「光速は観測者に依らない」が導く宇宙・世界観を,数学にしようとする。
そして出来たのが,「ミンコフスキー空間」である。
この文脈により,ミンコフスキー空間はつぎの要件を満たすようにつくられるものになる:
- 座標変換は,ローレンツ変換
- 内積は,ローレンツ変換で不変な内積
この要件から導かれた内積が,つぎのものである:
\[
\left(
\begin{array}{c}
c\,t_a \\
x_a \\
y_a \\
z_a \\
\end{array}
\right)
\cdot
\left(
\begin{array}{c}
c\,t_a \\
x_b \\
y_b \\
z_b \\
\end{array}
\right)
\ \ =\ \
\begin{array}{c}
t \\
\\
\\
\\
\end{array}
\left(
\begin{array}{c}
c\,t_a \\
x_a \\
y_a \\
z_a \\
\end{array}
\right)
\left(
\begin{array}{cccc}
-1 & & & \\
& 1 & & \\
& & 1 & \\
& & & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
c\,t_b \\
x_b \\
y_b \\
z_b \\
\end{array}
\right)
\\
\,
\\
\ \ \ \ \ \ =
- c^2\,t_a t_b + x_a x_b + y_a y_b + z_a z_b
\]
そしてこの内積を用いて,ベクトルの大きさ及び二点間の距離を定義する:
- ベクトル \( \bf a \) に対し,
\[
| \ {\bf a} | \,=\, \sqrt{ {\bf a} \cdot {\bf a} } \,=\, \sqrt{ - c^2\,t^2 + x^2 + y^2 + z^2 }
\]
- 二点A,Bに対し,
\[ \overline{AB} \,=\, | \vec{AB} | \]
この定義では,つぎの場合に \( | \bf{a} | \) が定義されない:
\[
- c^2\,t^2 + x^2 + y^2 + z^2 \,\ < \, 0
\]
しかしこれは,以下に示すように,不都合とはならない。
ct-xyz 座標を,原点を「いま・ここ」にとる。
そして,「いま・ここ」から見える世界を書き込む──図中の青色で表した円錐面 (図では断面の線) が,これである:
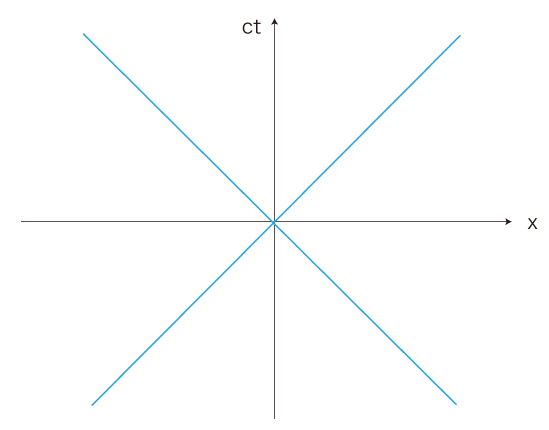
図は,ct - x 面を描いている
──この面と垂直にy軸とz軸がある
「いま・ここ」に届いている光を発した物質は曾てこの円錐面上に存在したものであり,曾てこの円錐面上に存在した物質が「いま・ここ」から見えている。
よってこの円錐面が,「いま・ここ」から見える世界である。
《物質Mからの光が「いま・ここ」に届いている》は,作図的に,2つ,且つ2つのみ,ある。
過去からのものが一つと,未来からのものが一つである。
Mは,この場合の<Mの過去>と<Mの未来>の間に存在するものとして思念される。
──実際,Mは<Mの過去>の前には存在していなかったかも知れないし,<Mの未来>の先には存在していないかも知れない。
そして,「<Mの過去>と<Mの未来>の間」は,つぎの領域にある:
\[
- c^2\,t^2 + x^2 + y^2 + z^2 \,\ \geqq \, 0
\]
そしてこの領域は,ベクトルの大きさの定義が成る領域と同じである。
これが「ミンコフスキー空間」である。
ここでは空間が4次元のところを2次元で描いてきたが,3次元的に表現しようとするとつぎの絵になる:
Wikipedia (「ミンコフスキー空間」) より引用
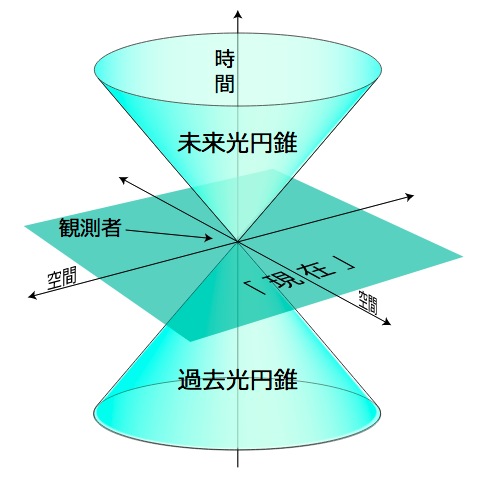
ミンコフスキー空間は,「時間」を「空間」と同じに見せ掛ける (→ 時空間)。
そのアイデアになっているのが,「時間表現と距離表現を重ねる」である:
《「c」を,「距離c」「光がc進む時間」の両義とする》
──そこで,光円錐の面の傾きが1になる。
|

