その移動を記述しようとする。 その方法は? 軌跡の図を書いてもだめである。 同じ軌跡を残す移動がいくらでもある。 方法は,《時間tをパラメータにして位置を表す》である:
方法の得は,失と表裏である。 この方法の難点は,記述から動きの像を起こすのが難しいことである。 動きをイメージするのが難しい。 動きの視覚的イメージ──即ち,絵──が欲しくなる。 動きがわかる絵。 こうして,空間と直交する時間軸を立てた絵の登場となる。 ただしこの絵は,3次元を模した描画のうちの1次元分を時間軸に譲ることになるので,空間は2次元 (平面) ないし1次元 (直線) に抽象されることになる。 この画法は,直線上の移動に対しては十全なものになる。 A点からB点への移動のいろいろが,互いに違って描かれることになる: 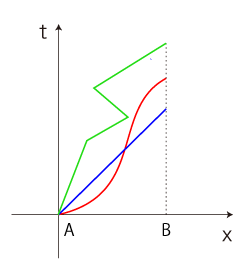
この絵の難点は,直線移動にしか使えない──t−x枠でしか使えない──ということである。 t−xy枠だと,見取り図ということになり,もはや解析の用途では使えない。──しかも,わけのわからない絵になってしまう: 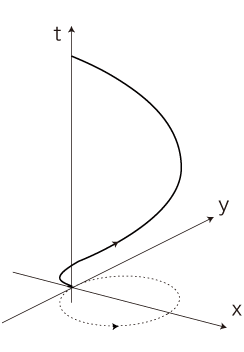
ミンコフスキー空間が解析の用途に足るのは,描く対象が,光の進行を含め,等速運動だからである。 等速運動だから一方向であり,運動をt- x 枠で描けることになるのである。 |