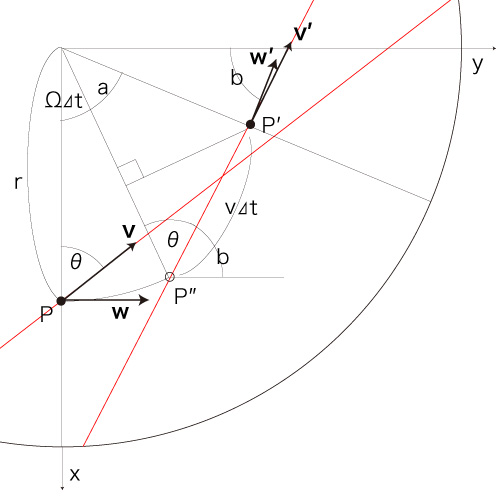
\[ v_x = - v\ cos( \theta )\\ v_y = v\ sin( \theta )\\ \ \\ \ \\ w_x = 0 \\ w_y = r\ \Omega \\ \] \[ v'_x = - v\ sin( b ) \\ v'_y = v\ cos( b ) \\ \] ここで \[ b + \theta + ( \pi / 2 - \Omega \Delta t ) = \pi \\ \Longrightarrow \ b = \pi / 2 - ( \theta - \Omega \Delta t ) \\ \ \\ cos( b ) = sin (\theta - \Omega \Delta t ) \\ \quad = sin(\theta) cos(\Omega \Delta t) - cos(\theta) sin(\Omega \Delta t) \\ \ \\ sin( b ) = cos ( \theta - \Omega \Delta t ) \\ \quad = cos(\theta) cos(\Omega \Delta t) + sin(\theta) sin(\Omega \Delta t) \] なので, \[ v'_x = - v\ sin( b ) = - v\ ( cos(\theta) cos(\Omega \Delta t) + sin(\theta) sin(\Omega \Delta t) ) \\ v'_y = v\ cos( b ) = v\ ( sin(\theta) cos(\Omega \Delta t) - cos(\theta) sin(\Omega \Delta t) ) \\ \] さらに, \[ \begin{align} w'_x = & - | {\bf{w'}} |\ sin( a + \Omega\ \Delta t ) \\ = & - ( \overline{ OP'}\ \Omega )\ ( sin(a)\ cos(\Omega \Delta t) + cos(a)\ sin(\Omega \Delta t) \\ \ \\ w'_y = & \ | {\bf{w'}} |\ cos( a + \Omega\\Delta t ) \\ = & \ ( \overline{ OP'}\ \Omega )\ ( cos(a)\ cos(\Omega \Delta t) - sin(a)\ sin(\Omega \Delta t) ) \\ \end{align} \] |