説明をネット検索してみると,どれもぐちゃぐちゃしていて (小難しいことを言っていて),ついていけない。 というわけで,説明を改めてつくってみることにする。 コマの運動は,「自転」である。 英語で言うと, "spin"。 自転は,半直線の運動に還元される。 半直線の端点が「自転の支点」というわけである。 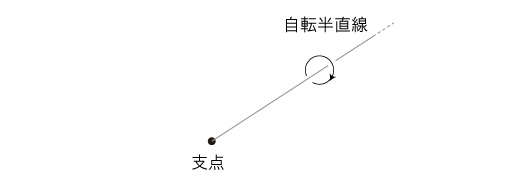
自転速度Ωは,つぎの3つによって表現される: このベクトルを,つぎのように表示する: 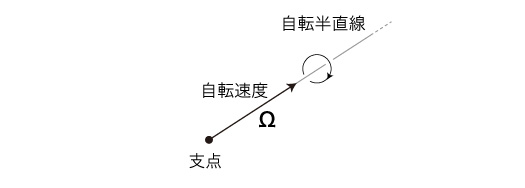
特に,半直線の向きと回転の大きさが同じで,回転方向が逆の2つの自転速度は,互いに逆ベクトルである: 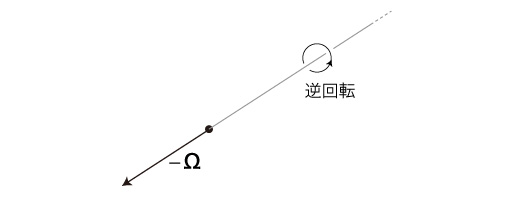
速度が定義されると,つぎに加速度が定義される。 即ち,自転速度の変化率として, 以上を準備したところで,「コマがなぜ倒れないか?」に入る。 コマの軸の2端点に,名前をつけよう:
自転しているコマは,傾いても倒れない。 そのかわり,頭は円運動している。 「コマはなぜ倒れないか?」の問いは,「コマの頭はなぜ円運動するか?」の問いに置き換わる。 時点tのコマの自転速度を,Ω(t) で表す。 時点tのコマは,つぎのようになっている: 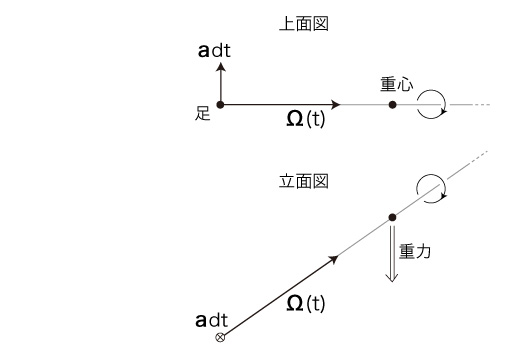
ここでaは自転加速度──「単位時間に変化する回転数はa」。 これは,<倒れる>から生じる:
(2) 方向が,倒れる面に垂直 <倒れる>は,時間 dt で自転速度が adt 増える運動である。 そこで,時点tの自転速度 Ω(t) と自転速度 adt の合成は,時点 t+ dt の自転速度 Ω(t+ dt ) を表す。 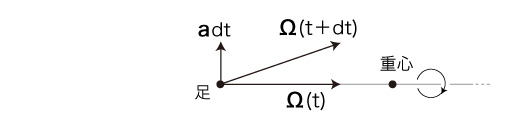
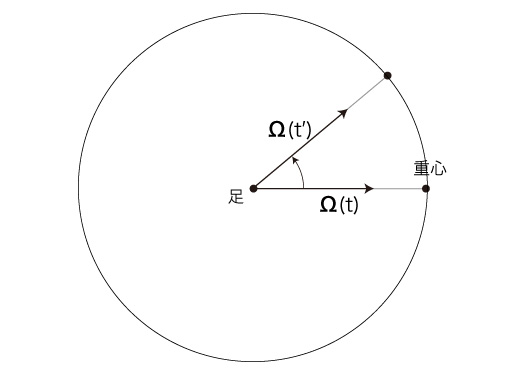
また,Ω(t) と adt から Ω(t+dt) が合成される図は,つぎのことも示している:
残るは,aの計算。 aは,つぎの3つで決まる: 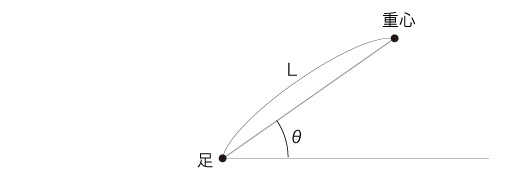
実際,重力加速度の大きさをgとすると,コマの質点にはつぎの力が作用している: 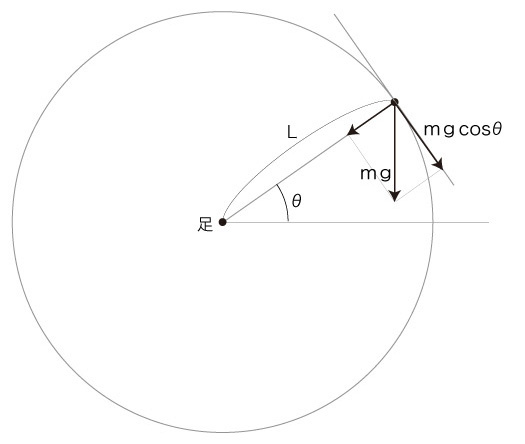
「速度 g cosθ」とは,「単位時間あたり移動距離が g cosθ」。 円上の移動距離 g cosθ は,g cosθ/(2πL) 回転に相当。 よって,「単位時間あたり移動距離が g cosθ」は,「単位時間あたり回転数が g cosθ/(2πL)」に相当。 よって,「単位時間あたり速度の変化が g cosθ」は,「単位時間あたり回転数の変化が g cosθ/(2πL)」に相当。 結局,
|