Up 「熱エネルギー・温度」の定義 作成: 2023-09-17
更新: 2023-09-17

    物を，つぎのようなものと考える：
      《この物にとっての＜最も乱雑な状態＞に向かって，
      　状態の乱雑さを単調に増している》

    この見方を，数理化する。
    そのために，
    1. ＜乱雑さ＞全体の集合，を立てる
    2. この集合に，「位」の代数的構造を入れる。
    これにより，「乱雑さ」が大小が言えるものになる。


    「位」の代数的構造は，アフィン空間である。
    「位」は，アフィン空間「点」である。
    アフィン空間は，ベクトル空間を内包する。
    これは，「位」でいうと，「位は量を内包する」ということである。
    つぎは，「位は量を内包する」の例：
      ＜時刻＞は，＜時刻の変化＝時間＞を内包する
      ＜高度＞は，＜高度の変化＝上下移動＞を内包する
      ＜位置＞は，＜位置の変化＝移動＞を内包する
      ＜温度＞は，＜温度の変化＝温度の上昇下降＞を内包する
    そしてこれらと同型に，
      ＜乱雑さ＞は，＜乱雑さの変化＞を内包する

    ことばにすると抽象的になるので，つぎの絵図で了解すべし：


    さて，物を
      《この物にとっての＜最も乱雑な状態＞に向かって，
      　状態の乱雑さを単調に増している》
    と定めたが，これはつぎのように表現される：
      《状態が乱雑であるほど，その状態になる確率が高い》
    そしてこれは，つぎのように言うのと同じ：
      《状態が乱雑であるほど，その状態の＜場合の数＞が大きい》

    この表現を，関数で表現する。
    即ち，各乱雑さ \( x \) に，それの場合の数 \( c_x \) の桁数──即ち，\( log\ c_x \) ──を対応させる関数を，\( f \) とする。

    \( f(x) \) を \( c_x \) ではなく \( log\ c_x \) にする理由は，
    • \( c_x \) だと値が大きくなり過ぎて，実用的なグラフにならない。
    • \( f(最大) = 0 \) になり，形がよい。
    • 後々，計算処理がうまくいく。

    f は，つぎのようになる：


    ここで，つぎの言い換えをする：
      「乱雑さ」→「熱エネルギー」
      「場合の数の桁数」→「エントロピー」

    これにより，これまで述べてきたことがつぎのようになる：
      物は，
        《この物にとっての＜最大の熱エネルギー＞に向かって，
        　熱エネルギーを単調に増している》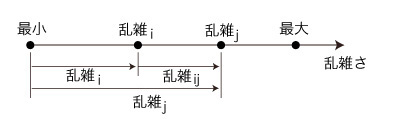


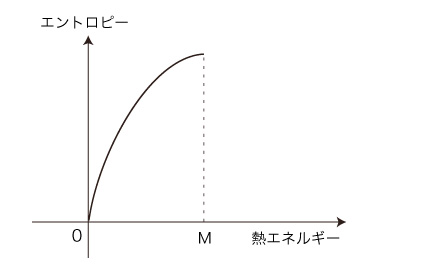
    ここで，いよいよ「温度」の導入となる。

    f のグラフの形に注目しよう。
    グラフは，変化率がつぎのようになっている：
    • 熱エネルギー０で，最大
    • 熱エネルギー最大で，０
    • その間，単調減少

    この変化率に，「温度」を見ることにする。
    「温度」のグラフは，つぎのようになる：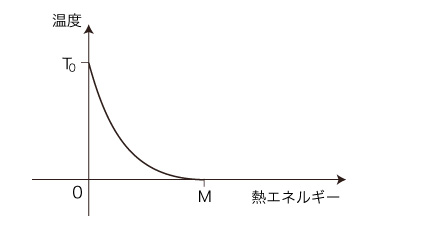
          \[ \frac{ d }{ dx } ( log c_x ) = \frac{ 1 }{ c_x } \frac{ d }{ dx } ( c_x ) \]

    物は，つぎにむけて単調に推移しているというわけである：
      ＜熱エネルギー最大 ≡ エントロピー最大 ≡ 温度０＞
    これは，「物の進化論」である。