Up 「価値」 作成: 2014-01-01
更新: 2014-01-02

    『資本論』は, 「価値」を実体的に定立する。
    ところで，『資本論』におけるこれの論述は，きわめて読みにくい。 これは，論述をすっきりさせるロジックが見出されてされていないためである。
    「価値」を定立する論述は，論述をすっきりさせるロジックが見出されてされていない体(てい) の論述である。

    今日だと，そのロジックは数学の「商集合・商構造」であることがわかる。
    マルクスの「価値」の構成法は，この数学を以て簡明に述べられるのである。
    また，この数学に照らすことで，併せて，「価値」概念の無理・観念性がはっきり見てとれるようになる。
    以下，このことを示す。


    1. 「類別」
    生活の中で「類別」(「仲間分け」) はよくあることだが，数学はこれがつぎの「〜」の規則になるものだということを捉える (「〜」は「同類」ないし「仲間」と読むとよい)：
      1゜ｘ〜ｘ
      2゜ｘ〜ｙ ならば y〜ｘ
      3゜ｘ〜ｙかつｙ〜ｚ ならば ｘ〜ｚ
      　 （「ｘとｙが同類でｙとｚが同類ならば，ｘとｚは同類」）
    即ち，集合Ａの要素の間に「〜」の関係があれば，集合Ａの要素は「〜」によって類別される。
    「〜」は，「同値関係」と呼ばれる。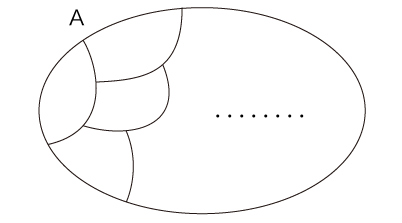



      例：自然数 1, 2, 3, ‥‥ の集合において，つぎの「〜」は同値関係：
        自然数ｘ, ｙに対し，「ｘ〜ｙ」を「ｘ, ｙを３で割った余りは同じ」の意味とする。
        （「ｘ, ｙを３で割った余りは同じ」は，「ｘとｙの差は３の倍数」と言っても同じ。）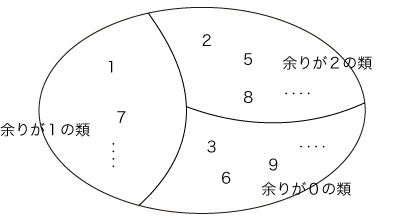
      このとき，自然数の集合は，３つの類に分けられる──余りが０の類，余りが１の類，余りが２の類。


    「価値」の構成では，集合Ａとして，人が交換し合う商品の集合を考える。
    そして，つぎの「〜」を，Ａにおける同値関係と見なす：
      商品ｘ, ｙに対し，「ｘ〜ｙ」を「ｘとｙは交換される」の意味とする。
    この「〜」によって，集合Ａは類別される。──交換可能な商品どうしの類に分けられる。



    2. 「商集合」
    集合Ａは，同値関係「〜」によって，類別された。
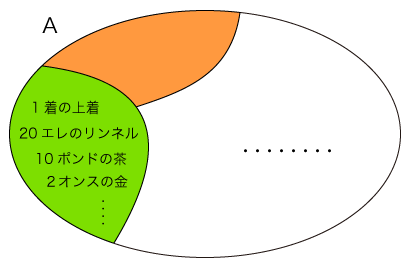    ここで，類を要素とする集合を考える。
    これを「Ａ/〜」で表し，「同値関係〜に関するＡの商集合」と呼ぶ。
    Ａの要素ｘの属する類を [ｘ] で表す。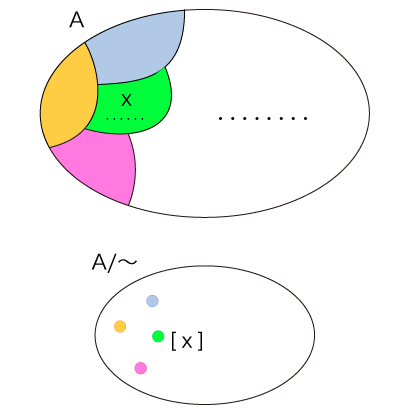


    集合Ａとして人が交換し合う商品の集合を考え，「互いに交換される」を同値関係「〜」と見なした。 そして，Ａを交換可能な商品どうしの類に分けた。
    ここで，集合Ａ/〜 (交換可能な商品どうしの類を要素とする集合) を考える。
    そして，Ａ/〜 の要素を「価値」と定める。
    商品ｘに対する [ｘ] が，「ｘの価値」である。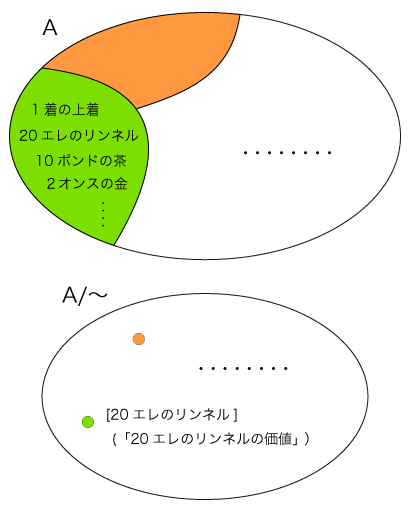


    3. 「代数的構造」
    集合Ａの要素の間に和「＋」が定義されているとき，これはＡ/〜 の要素の間の和を導く：
        [ｘ] ＋ [ｙ] ＝ [ｘ＋ｙ]

    集合Ａとして人が交換し合う商品の集合を考え，「互いに交換される」を同値関係「〜」と見なした。 そして，商集合Ａ/〜 を以て「価値」を定義した。 このとき，商品ｘに対する [ｘ] が，「ｘの価値」である。
    ところで，商品ｘと商品ｙを合わせたものは，交換にのるところのまた一つの商品である。即ち，Ａの要素には和「＋」が定義される。
    この和は，Ａ/〜 の要素の和，即ち価値の和を導く。
        [ｘ] ＋ [ｙ] ＝ [ｘ＋ｙ]


    以上，『資本論』における「価値」の定立の仕方を，数学に照らして，明らかにしてきた。
    そして数学に照らすことで，併せて，「価値」概念の無理・観念性が併せて見てとれることにもなる。
    即ち，「価値」構成の出発点は「互いに交換される」を同値関係「〜」と見なすことであったが，これは無理であり観念論である。
    翻って，『資本論』の「価値」論は，「価値」を規範として立てる論である。