Up コマの物理──角運動量 作成: 2022-04-12
更新: 2023-02-05

    「角運動量」がおさまる物理学は，コマの物理学である。

    コマの運動は，「自転」である。
    英語で言うと, "spin"。

    自転(スピン)は，円運動とは違う。
    固有の運動として考えるものである。


    自転は，半直線の運動に還元される。
    半直線の端点が「自転の支点」というわけである。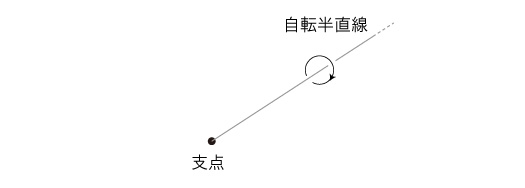

    　　註： 地球の自転の場合は，地球の中心を端点とし北極を通る半直線が，ふつうとられる。


    直進運動に対しては，「速度」を導入した。
    円運動は，微分によって直進運動に表現されるので，直進運動の速度がこれの速度になる。
    同様に，自転運動に対しても「速度」──「自転(スピン)速度」──を考えることにする。

    即ち，自転速度Ωを，支点から無限遠点を見たときの自転の角速度 (ベクトル) ── 右回りか左回りか，単位時間あたり何ラジアンか ──で定義する。
    そして，つぎのようにベクトル表現する：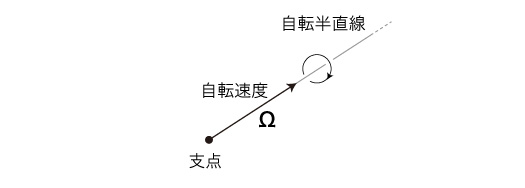
    1. ベクトルの大きさは，角速度の大きさ
    2. ベクトルの向きは，
支点から無限遠点を見て右回りのとき：

支点から無限遠点を見て左回りのとき：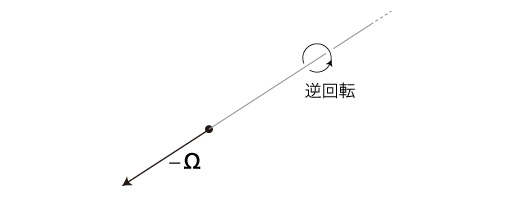


    自転する半直線に，質点と質量を考える。
    直進運動で質量と速度の積として運動量を定義したように，質量と自転速度の積として自転運動量 (ベクトル) を定義する。

    こうして定義した自転運動量が，「角運動量」である。
    （自転速度が角速度で定義されたので，自転運動量は「角運動量」ということになる！)


    「角運動量」は，自転 (スピン) の運動量である。
    円運動の運動量 (これは微分によって直進運動の運動量に表現される) と混同しないこと。