気圧モデルは,「空気分子が飛んで来て衝突」。 そして水圧モデルは,「水分子が密着して圧迫」になる。 はじめに,雑駁なモデルから。 水の中に,立方体の区画 A1, A2, A3, ‥‥ を,つぎのように考える: 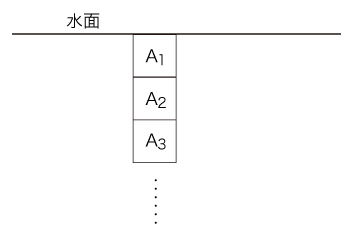
A1, の上面には,大気圧 F0 がかかっている。 A2, の上面には,F0 に A1 の重さを加えた力 F1 がかっている。 A3, の上面には,F1 に A2 の重さを加えた力 F2 がかっている。 ‥‥
各 An の水塊は,その内部に水の流れがない状態で形を保っているとしよう。 これは,つぎのような力の釣り合いが実現されているということである 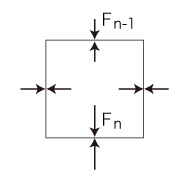
横方向の力の大きさは? これは縦方向の力の大きさと等しい (圧力の等方性)。 実際,等しくなければ,An の中で水の流れが生じることになる──圧力の高いところから低いところへ。 ただし横方向の力の大きさは,An の上面から下面へ Fn−1 から Fn に推移する。 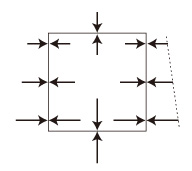
以上は,離散モデルである。 これを連続モデルに変える。 立方体のサイズを →0 にするわけである。 この結果は,つぎのようになる:
水深nメートルの一点には,f + ρn トン重/m2 の圧力がかかる。 大気圧は約10トン重/m2,水の密度は1トン/m3 なので,
水圧のモデルは,「重力による収縮と圧力勾配による膨張とが釣り合う」である。 「重力による収縮と圧力勾配による膨張とが釣り合う」は,「静水圧平衡」と呼ばれる。 また,「重力による収縮と圧力勾配による膨張とが釣り合う」を一般的に考えるときは,これを「静力学平衡」と呼ぶ。 |