Up \( (S_a, P_a) \) の定義 作成: 2022-10-03
更新: 2022-10-04

    位置 \( P \) と速度 \( \bf{v} \) の対から，\( (P, \bf{v} ) \) -座標を定義した。
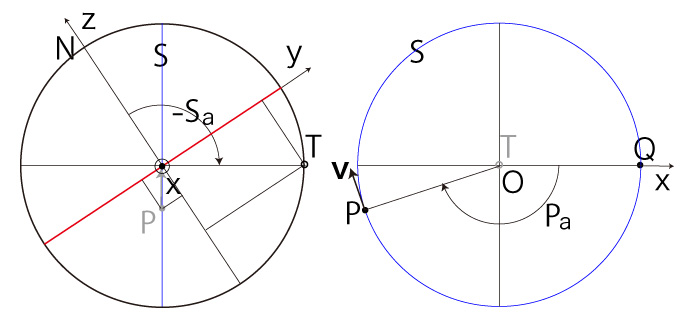
    ここでは，\( P,\ \bf{v} \) の座標を表現するためのパラメータ \( (S_a, P_a ) \) を導入する。


    \( (P, \bf{v} ) \)-法点を \( T \) とする。
    そして，回転角度 \( S_a,\ P_a \) をつぎのように定義する：
    • \( O \) から \( T \) を見て，\( OQ \) から \( OP \) までの右回転角度を，\( P_a\ ( 0 \leqq P_a < \pi ) \) とする。
    • \( O \) からｘ軸の正の方向を見て，\( ON \) から \( OT \) までの右回転角度を，\( S_a\ ( - \pi < S_a < \pi ) \) とする。


    　註： \( ON \) から \( OT \) までの右回転角度が \( \pi \) を超え，左回転角度が \( \theta < \pi \) であるときは，\( - \theta \) が \( S_a \) になる。
    以下に示すように，こうなるのは \( P \) が南半球にある場合である。



    以下に，\( P\, T \) の座標と \( ( S_a,\ P_a ) \) の対応を示す：

    \( P_z > 0 \) の場合──即ち，\( P \) が北半球にある場合

    \( P_x \geqq 0,\ P_y \geqq 0 \) のとき，

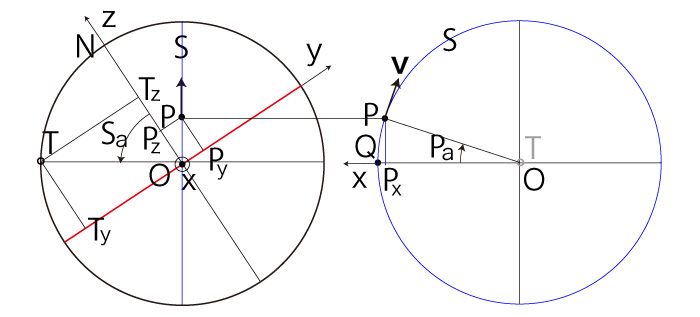
    \( P_x \geqq 0,\ P_y < 0 \) のとき，

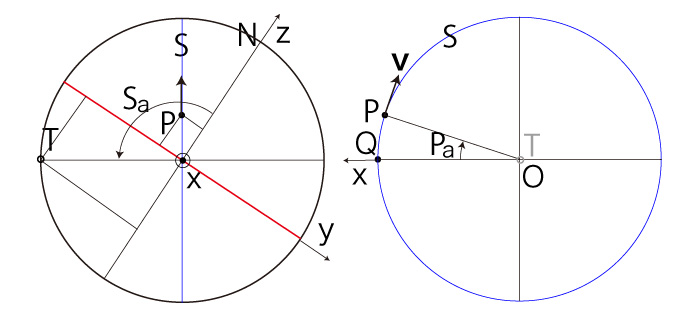
    \( P_x < 0,\ P_y \geqq 0 \) のとき，

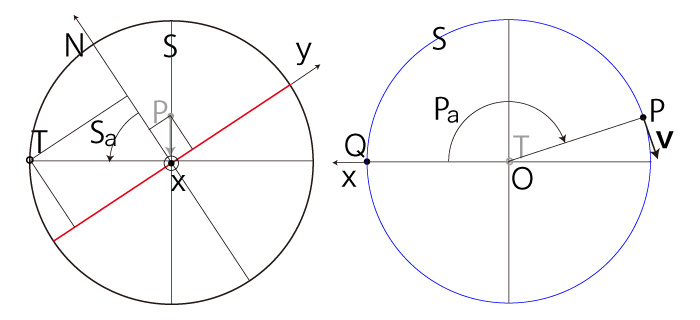
    \( P_x < 0,\ P_y < 0 \) のとき，

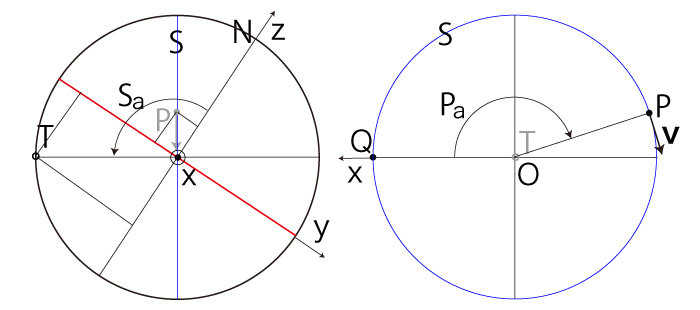
    \( P_z < 0 \) の場合──即ち，\( P \) が南半球にある場合

    \( P_x \geqq 0,\ P_y \geqq 0 \) のとき，
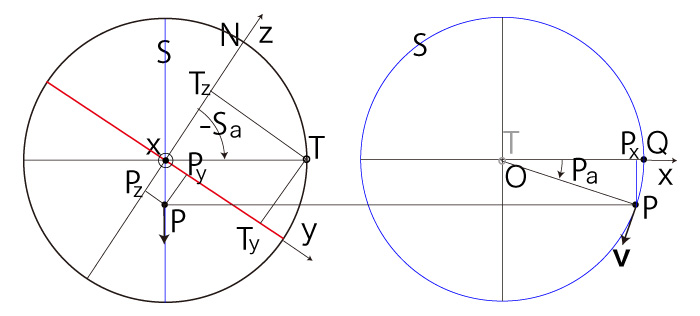
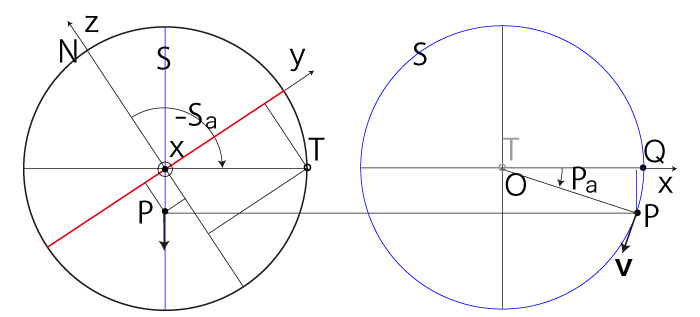
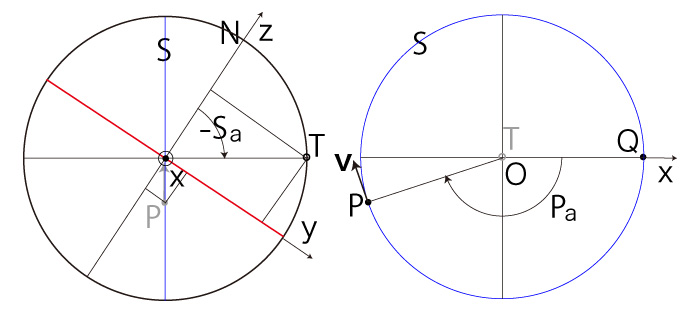
    \( P_x \geqq 0,\ P_y < 0 \) のとき，
    \( P_x < 0,\ P_y \geqq 0 \) のとき，
    \( P_x < 0,\ P_y < 0 \) のとき，