Up

\( P \) での回転速度 \( \bf{w} \) の \( (S_a, P_a) \) 表現

作成: 2022-06-26 更新: 2022-10-11

---

球体の自転の角速度を \( \Omega \) とする。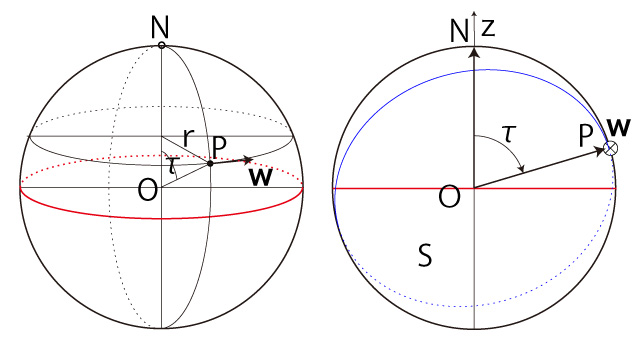 \( {\bf w} \) は， (1) \( P \) が極のとき── \( P = ( 0,\ 0,\ \pm R ) \) のとき ──は， \[ {\bf w} = 0 \\ \] (2) \( P \) が極でないときは， \( \vec{ON} \) から \( \vec{OP} \) への回転角度を \( \tau\ ( 0 < \tau < \pi ) \)，\( P \) からｚ軸までの距離を \( r \) とするとき， \[ {\bf w} = | {\bf w} |\ \frac{ \vec{ON} \times \vec{OP} }{ | \vec{ON} \times \vec{OP} |} \\ | {\bf w} | = r\ \Omega \\ r = R\ sin( \tau ) \\ \] \( N,\ P \) の座標が \[ N_x = 0, \\ N_y = 0 \\ N_z = R \\ \ \\ P_x = R\ cos( P_a ) \\ P_y = R\ sin( P_a )\ cos( S_a ) \\ P_z = R\ sin( P_a )\ sin( S_a ) \] なので， \[ \begin{align} \vec{ON} \times \vec{OP} & = ( N_x,\ N_y,\ N_z ) \times (P_x,\ P_y,\ P_z )\\ & = (N_y\ P_z - N_z\ P_y,\ N_z\ P_x - N_x\ P_z,\ N_x\ P_y - N_y\ P_x ) \\ \ \\ & = (0\ R\ sin( P_a )\ sin( S_a ) - R\ R\ sin( P_a )\ cos( S_a ), \\ & \quad R\ R\ cos( P_a ) - 0\ R\ sin( P_a )\ sin( S_a ), \\ & \quad 0\ R\ sin( P_a )\ cos( S_a ) - 0\ R\ cos( P_a ) ) \\ \ \\ & = R^2 (- sin( P_a )\ cos( S_a ),\ cos( P_a ),\ 0 ) \end{align} \] そして， \[ | \vec{ON} \times \vec{OP} | = | \vec{ON} |\ | \vec{OP} |\ sin( \tau ) = R^2\ sin( \tau ) = R\ r \\ \] よって，\( {\bf w} = ( w_x,\ w_y,\ w_z ) \) は， \[ w_x = - R \Omega\ cos( S_a )\ sin( P_a ) \\ w_y = R \Omega\ cos( P_a ) \\ w_z = 0 \\ \]