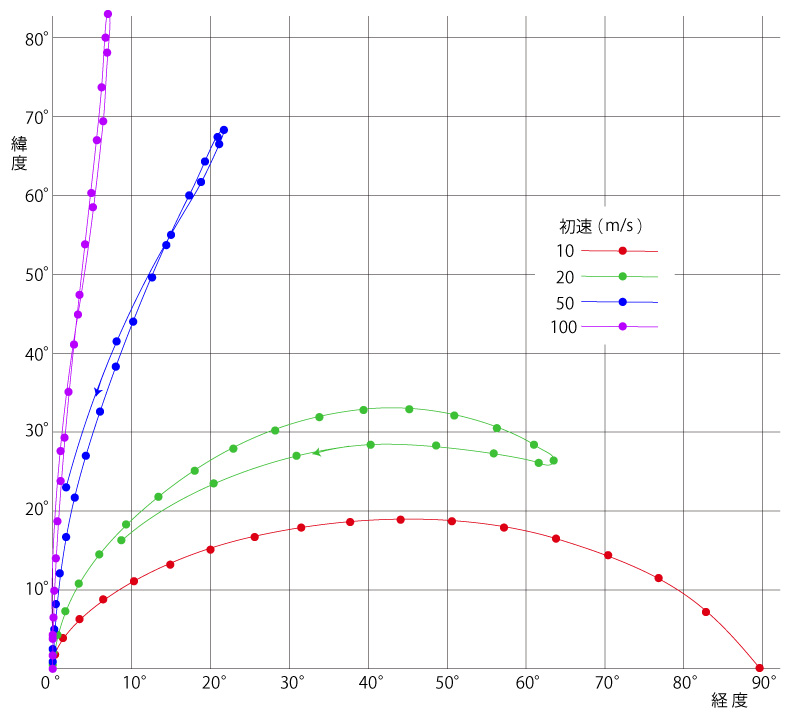
初速 10m/s
|
緯度 |
経度 |
速度 |
| 0 |
0.0 |
0.0 |
10 |
| 1 |
0.5 |
0.0 |
61 |
| 2 |
1.8 |
0.3 |
120 |
| 3 |
3.9 |
1.3 |
175 |
| 4 |
6.3 |
3.4 |
225 |
| 5 |
8.8 |
6.4 |
268 |
| 6 |
11.1 |
10.3 |
305 |
| 7 |
13.2 |
14.9 |
337 |
| 8 |
15.1 |
20.0 |
362 |
| 9 |
16.7 |
25.6 |
383 |
| 10 |
17.9 |
31.5 |
399 |
| 11 |
18.6 |
37.7 |
413 |
| 12 |
18.9 |
44.1 |
424 |
| 13 |
18.7 |
50.6 |
433 |
| 14 |
17.9 |
57.2 |
441 |
| 15 |
16.5 |
63.8 |
448 |
| 16 |
14.4 |
70.4 |
454 |
| 17 |
11.5 |
76.8 |
459 |
| 18 |
7.2 |
82.8 |
462 |
| 19 |
0.1 |
89.6 |
464 |
| |
初速 20m/s
|
緯度 |
経度 |
速度 |
| 0 |
0.0 |
0.0 |
20 |
| 1 |
0.6 |
0.0 |
64 |
| 2 |
2.0 |
0.1 |
121 |
| 3 |
4.3 |
0.6 |
175 |
| 4 |
7.3 |
1.6 |
225 |
| 5 |
10.8 |
3.3 |
268 |
| 6 |
14.5 |
5.9 |
305 |
| 7 |
18.3 |
9.3 |
336 |
| 8 |
21.8 |
13.4 |
361 |
| 9 |
25.1 |
18.0 |
381 |
| 10 |
27.9 |
22.9 |
398 |
| 11 |
30.2 |
28.2 |
413 |
| 12 |
31.9 |
33.8 |
426 |
| 13 |
32.8 |
39.4 |
438 |
| 14 |
32.9 |
45.2 |
450 |
| 15 |
32.1 |
50.9 |
463 |
| 16 |
30.5 |
56.3 |
476 |
| 17 |
28.4 |
61.0 |
490 |
| 18 |
26.4 |
63.5 |
506 |
| 19 |
26.1 |
61.6 |
525 |
| 20 |
27.3 |
55.9 |
551 |
| 21 |
28.3 |
48.6 |
587 |
| 22 |
28.4 |
40.3 |
638 |
| 23 |
27.0 |
30.9 |
713 |
| 24 |
23.5 |
20.4 |
824 |
| 25 |
16.3 |
8.7 |
989 |
| 26 |
1.9 |
-0.1 |
1235 |
| |
初速 50m/s
|
緯度 |
経度 |
速度 |
| 0 |
0.0 |
0.0 |
50 |
| 1 |
0.9 |
0.0 |
78 |
| 2 |
2.5 |
0.0 |
128 |
| 3 |
5.0 |
0.2 |
180 |
| 4 |
8.2 |
0.4 |
227 |
| 5 |
12.1 |
0.9 |
269 |
| 6 |
16.7 |
1.7 |
305 |
| 7 |
21.7 |
2.8 |
334 |
| 8 |
27.0 |
4.2 |
358 |
| 9 |
32.6 |
6.0 |
378 |
| 10 |
38.3 |
8.0 |
394 |
| 11 |
44.0 |
10.2 |
409 |
| 12 |
49.6 |
12.6 |
423 |
| 13 |
55.0 |
15.0 |
439 |
| 14 |
60.0 |
17.3 |
457 |
| 15 |
64.3 |
19.3 |
481 |
| 16 |
67.4 |
20.9 |
513 |
| 17 |
68.3 |
21.7 |
557 |
| 18 |
66.5 |
21.1 |
621 |
| 19 |
61.7 |
18.8 |
717 |
| 20 |
53.7 |
14.4 |
862 |
| 21 |
41.5 |
8.1 |
1092 |
| 22 |
23.0 |
1.7 |
1467 |
| |
初速 100m/s
|
緯度 |
経度 |
速度 |
| 0 |
0.0 |
0.0 |
100 |
| 1 |
1.7 |
0.0 |
116 |
| 2 |
3.8 |
0.0 |
152 |
| 3 |
6.5 |
0.1 |
194 |
| 4 |
9.9 |
0.2 |
236 |
| 5 |
14.0 |
0.4 |
273 |
| 6 |
18.7 |
0.6 |
306 |
| 7 |
23.8 |
1.0 |
332 |
| 8 |
29.3 |
1.5 |
354 |
| 9 |
35.1 |
2.0 |
371 |
| 10 |
41.1 |
2.7 |
386 |
| 11 |
47.4 |
3.4 |
398 |
| 12 |
53.8 |
4.1 |
410 |
| 13 |
60.3 |
4.9 |
423 |
| 14 |
67.0 |
5.6 |
439 |
| 15 |
73.7 |
6.2 |
459 |
| 16 |
80.0 |
6.7 |
487 |
| 17 |
83.0 |
7.0 |
526 |
| 18 |
78.1 |
6.9 |
582 |
| 19 |
69.4 |
6.3 |
664 |
| 20 |
58.5 |
5.1 |
787 |
| 21 |
44.9 |
3.2 |
974 |
| 22 |
27.6 |
1.0 |
1265 |
| 23 |
4.3 |
0.0 |
1737 |
|
 プログラムのテスト ) を,そのままグラフにしたものである。
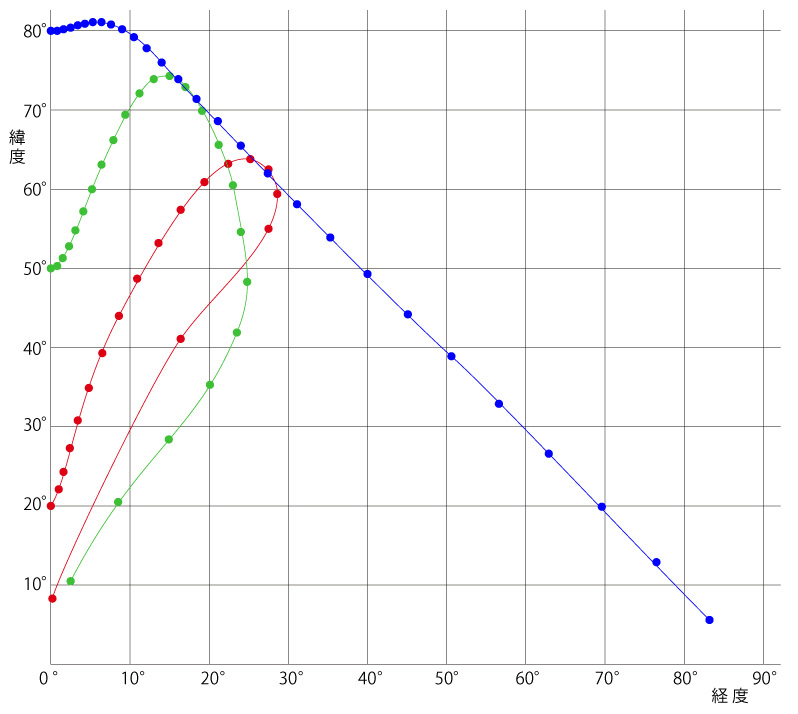
プログラムのテスト ) を,そのままグラフにしたものである。