Up なぜ「\( (P, {\bf{v}} ) \)-座標」か 作成: 2022-06-26
更新: 2022-09-28

    球体の表面を直進する。
    この移動の軌跡は，大円になる。

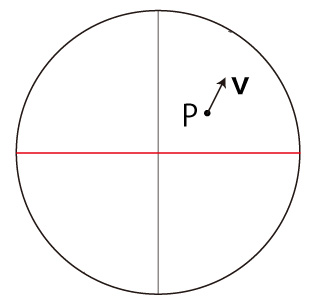
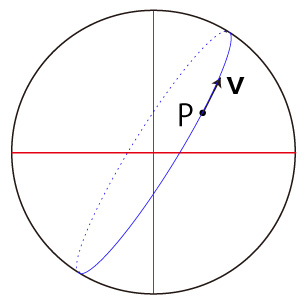
    しかしここで，球体が自転する球体だとする。
    このとき，移動は球体の自転と重なる。
    その移動は, つぎのようになる：
      《その都度 (即ち，位置 \( P \) とそこでの速度 \( {\bf{ v }} \) に応じて) 加速度を呼び込む》

    この移動をとらえためには，\( P,\ {\bf{ v }} \) に応じる加速度がわからねばならない。
    そこでこの加速度を求めようとする。


    この加速度を，つぎのように分析する：
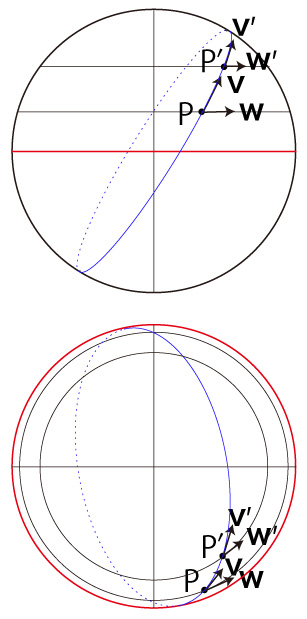      《加速度は，速度 \( {\bf v} \) と球体の自転による回転速度 \( {\bf w} \) を，それぞれ\( {\bf v'},\ {\bf w'} \) に変化させる》

    こうして，つぎが求めようとする加速度である：
        \[ \frac{ ( {\bf v'} + {\bf w'} ) - ( {\bf v} + {\bf w} ) }{ \Delta t } \quad \quad ( \Delta t \longrightarrow 0 ) \]


    加速度の計算は，移動の位置と速度を表すための座標系を設定するところから始まる。
    座標系は，いまの位置 \( P \) と速度 \( {\bf{ v }} \) をもとにしてつくることになる。

    このとき，つぎの座標系が自然な感じがする：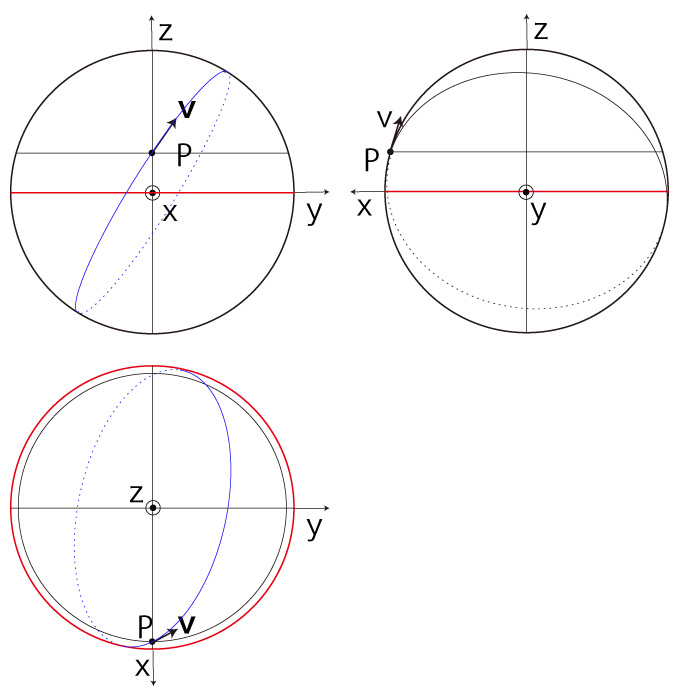
    しかしこれはダメである。
    計算が手に負えなくなるのである。
    加速度の計算は，座標のパラメータを上手にとっていかないと，計算が手に負えなくなる。

    実際，座標パラメータの取り方はほとんど "uniquely determined" となりそうである。
    本節「座標系」では，その座標系を──「\( ( P, {\bf{ v }} ) \) 座標系」の名で──導入する。