問題:ここに高低差が同じ3つのスロープがある。
上から玉を転がすとき,いちばんスピードが出るスロープはどれ?
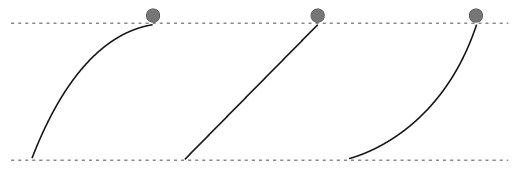
|
これは,引っ掛け問題である。
どんなタイプの者が引っ掛けの対象かというと,学校で「落下速度」を学んだ者である。
彼らはつぎのように学んだ:
| 「 |
落下速度は高低差で決まる。
実際,高低差は位置エネルギーの差を示し,そして落下は,<高さ>に示される位置エネルギーを運動エネルギーに変換するダイナミクスである。
そしてこの変換を計算すると,速度は高低差だけで決まり,物体の質量にも依らない。」
|
これが偏って身につくと,ポテンシャル主義者──行程を閑却するワープ主義者──になる。
先の問題は,この彼らに対する引っ掛け問題なのである。
彼らは,「高低差が同じなので同じ速さ!」と答える。
実際は,各スロープを相手に,個別に計算して答えを出すしかない。
計算は,微小に区分された<位置エネルギーから運動エネルギーへの変換で導かれる速度>──これは傾斜に依存──を積んでいく計算である。
この作業に近道は無い。
大気の移動の計算も,もしやろうとするならばだが,これと同じ格好になる。
途方も無い作業になることは,目に見えている。
実際,本サイトは,
<最も単純な設定&移動物体の捨象>をした「速度ベクトルの移動方程式」
の作業だけでも,どのくらいのものになるかを示してきた。
しかし気象学は,「大気の移動」の主題においてポテンシャル主義/ワープ主義者である。
気象学は,大気に「角運動量」というポテンシャルをもたせ,大気の速度をこのポテンシャルの増減で説明しようとする。
気象学は,「落下する物体の速度は,落下距離 (高低をどれだけワープしたか) で決まる」のように,「移動する大気の速度は,緯度をどれだけワープしたかで決まる」と唱えるのである。
実例として,Hartmann (2016) のテクストを引用しておく。
──「赤道上で停止の空気塊を北緯30° までワープさせると 134m/秒の速さで東向きに回る」を教えている。
| |
Hartmann (2016), §6.3.1
Wind velocities in the atmosphere are measured in terms of a local Cartesian coordinate system inscribed on a sphere.
At each latitude \( \phi \) and longitude λ on a sphere of radius a, the zonal and meridional components of horizontal velocity
are defined in the following way (Fig.6.3):
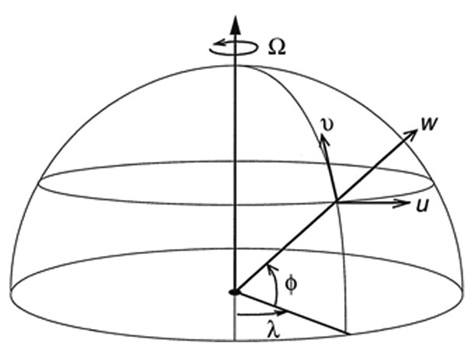 Figure 6.3
Figure 6.3
Local Cartesian coordinates on a sphere and
the zonal (u), meridional (v), and vertical (w)
components of the local vector wind velocity.
\[
u = a\ cos\phi\ \frac{ D \lambda }{ D t } = \rm{ zonal\ or\ eastward\ wind\ speed }
\]
\[
v = a\ \frac{ D \phi }{ D t } = \rm{ meridional\ or\ northward\ wind\ speed\ \quad \quad } (6.4)
\]
Here D/ Dt represents the material derivative – the temporal tendency that is experienced by an air parcel moving with the flow.
|
|
| |
Hartmann (2016), §6.4
|
The zonal velocity of Earth’s surface at the equator, about \( 465 ms^{−1}\), is very large compared to typical zonal wind speeds in the atmosphere.
\[
\begin{align}
u_{earth} &= Ω\ a\ cos\phi \\
&= 7.292 × 10^{−5}\ rad\ s^{−1} \times 6.37 \times 10^6\ m ⋅ cos\phi \\
&= 465\ m\ s^{−1} \times cos\phi \\
\end{align}
\]
The atmospheric angular momentum associated with Earth’s rotation is thus much larger than the angular momentum associated with the zonal winds normally observed in the troposphere.
When air parcels move poleward in the atmosphere, they retain the same angular momentum unless they exchange angular momentum with other air parcels or with the surface.
Since the distance to the axis of rotation of Earth decreases as a parcel moves poleward on a level surface, the relative eastward zonal velocity of the parcel must increase to maintain a constant total angular momentum.
Thus, poleward-moving parcels experience an eastward acceleration relative to Earth’s surface.
If a parcel of air moves from one latitude to another while conserving angular momentum, then (6.15) implies a relationship between the zonal velocities the parcel will have at any two latitudes.
\[
\begin{align}
M &= ( Ω\ a\ cos\phi_1 + u_1)\ a\ cos\phi_1 \\
&= ( Ω\ a\ cos\phi_2 + u_2)\ a\ cos\phi_2 \quad \quad (6.16) \\
\end{align}
\]
If a parcel starts out at the equator with zero relative velocity and moves poleward to another latitude while conserving its angular momentum, we have from (6.16) that
\[
M = Ω\ a^2 = ( Ω\ a\ cos\phi + u_\phi)\ a\ cos\phi \quad \quad (6.17)
\]
which can be rearranged to yield an expression for the zonal velocity at any other latitude \( u_\phi \),
\[
u_\phi = Ω\ a\ \frac{ sin^2\phi }{ cos\phi } \quad \quad (6.18)
\]
By substituting numbers into (6.18) we find that a parcel of air with the angular momentum of Earth’s surface at the equator will have a westerly zonal wind speed of \( 134 ms^{−1} \) at 30°N or 30°S.
This is much greater than the maximum zonally averaged wind speeds in the subtropical jet stream (Fig.6.4), and we infer that the poleward angular momentum transport in the upper, poleward-flowing branch of the Hadley cell is more than adequate to explain the existence of a \(40 ms^{−1} \) jet at 30 ° latitude.
The interesting part is explaining why the subtropical jet stream is not stronger than it is.
|
|
- 引用/参考文献
- Hartmann, D.L. (2016) : Global Physical Climatology (Sec. Ed.). Elsevier.
|

