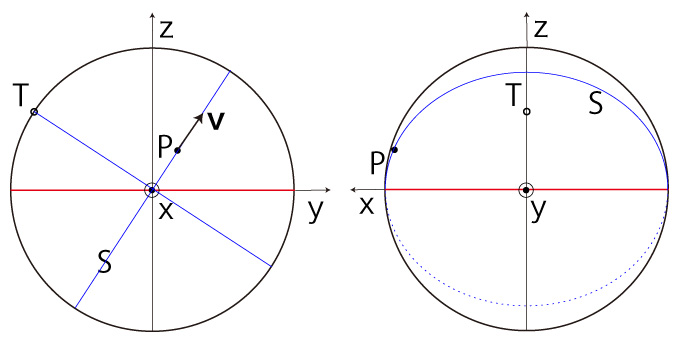
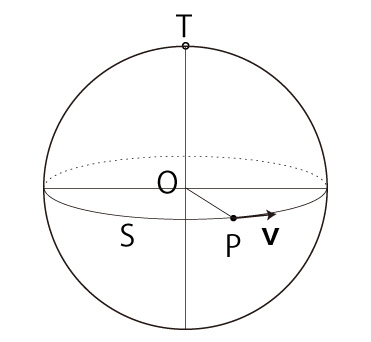
\( (P, {\bf{v}} ) \)-大円 \( S \) の位相 (phase) の表現は,球面上の点 \( T \) で \( \overrightarrow{OT} \) が \( S \) の法線ベクトルとなるものの位相の表現に換えられる。
そして表現は,後者が簡潔になる。
この \( T \) を,\( (P, {\bf{v}} ) \)-法点と呼ぶことにする。
| 定義: |
球面上の点 \( T \) で \( \overrightarrow{OT} \) が \( S \) の法線ベクトルとなるものは2点あるが,\( O \) からその点を見たときの \( \{\bf{v} \) 方向回転が右回転になるものを,\( (P, {\bf{v}} ) \)-法点と呼ぶ。
|
.
|