\( ( P, \bf{v} \)-法点は,この2点のどちらかである。 そしてどちらであるかを決めるのは,\( \bf{v} \) の方向である。 しかし,つぎの2つの条件が満たされるとき,\( T \) の座標は \( P \) の座標のみによって表現される。 これは,\( ( P,\bf{v} ) \)-座標のつぎの性質に因る:
\( T_z \) と \( P_y \) は,同符号 逆に,\( P_y \) か \( P_z \) が0のとき,\( T \) が決まらなくなる。 それが上の逆条件のつぎの場合であり,\( \bf{v} \) の座標が要ることになる。 以下,各場合について,その内容を見ていく。 これは,\( P_x = R,\ P_y = P_z = 0,\ v_x = v_y = 0 \) の場合である。 そしてこれは,\( T \) が極になっている場合,即ち \( T_y = 0,\ T_z = \pm R \) の場合である。 このとき \( T_z \) が \( \pm R \) のいずれであるかを決めるのは,赤道に乗っている \( \bf{v} \) の方向,即ち \( v_y \)。 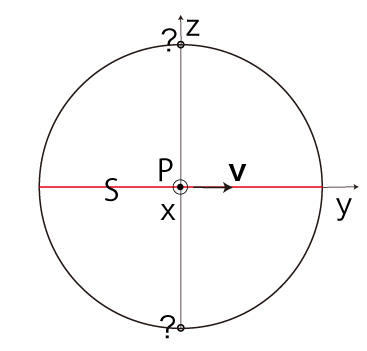
これは,\( P_y = 0,\ v_y = 0 \) の場合である。 そしてこれは,これは,\( T_y = \pm R,\ T_z = 0 \) の場合である。 このとき \( T_y \) が \( \pm R \) のいずれであるかを決めるのは,経線に乗っている \( \bf{v} \) の方向,即ち \( v_z \)。 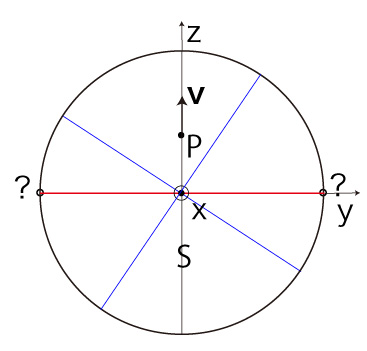
これは,\( P_x = \pm R,\ P_y = P_z = 0 \) の場合である。 また,このとき \( T \) が定まるためには,\( v_y,\ v_z \) の両方が定まらねばならない。 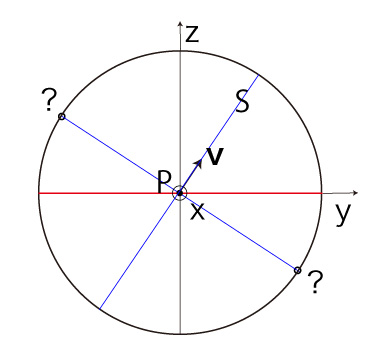
\( T \) の座標 \( ( T_x,\ T_y,\ T_z ) \) は,\( T_x = 0 \) である。 \( T_y,\ T_z \) については \[ P_y\ T_y + P_z\ T_z = 0 \\ T_y^2 + T_z^2 = R^2 \] から, \[ P_y^2\ T_y^2 = P_z^2\ T_z^2 = P_z^2\ ( R^2 - T_y^2 ) = P_z^2\ R^2 - P_y^2\ T_y^2 \\ P_z^2\ T_z^2 = P_y^2\ T_y^2 = P_y^2\ ( R^2 - T_z^2 ) = P_y^2\ R^2 - P_y^2\ T_z^2 \\ \ \\ \ \\ \ ( P_y^2 + P_y^2 )\ T_z^2 = P_z^2\ R^2 \\ \ ( P_y^2 + P_z^2 )\ T_z^2 = P_y^2\ R^2 \\ \ \\ \ \\ ( R^2 - P_x^2 )\ T_y^2 = P_z^2\ R^2 \\ ( R^2 - P_x^2 )\ T_z^2 = P_y^2\ R^2 \\ \] \( R^2 - P_x^2 \ne 0 \) なので, \[ T_y^2 = R^2\ \frac{ P_z^2 }{ R^2 - P_x^2 } \\ T_z^2 = R^2\ \frac{ P_y^2 }{ R^2 - P_x^2 } \\ \] そして
\( T_z \) と \( P_y \) は,同符号 \( P_z > 0 \) の場合──即ち,\( P \) が北半球にある場合 \( P_x \geqq 0,\ P_y \geqq 0 \) のとき, |
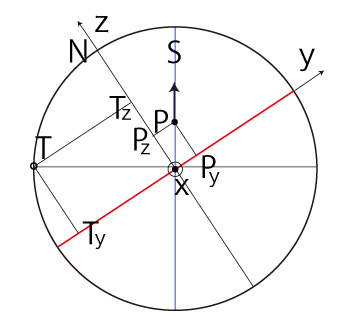
\( P_x \geqq 0,\ P_y < 0 \) のとき, |
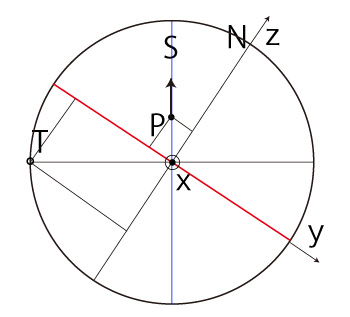
\( P_x < 0,\ P_y \geqq 0 \) のとき, |
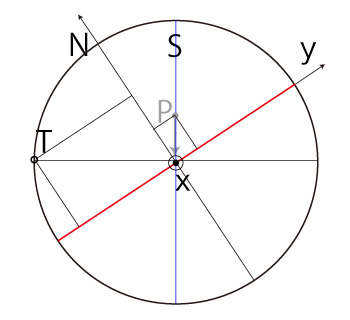
\( P_x < 0,\ P_y < 0 \) のとき, |
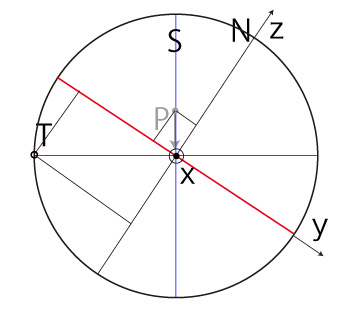
\( P_z < 0 \) の場合──即ち,\( P \) が南半球にある場合 \( P_x \geqq 0,\ P_y \geqq 0 \) のとき, |
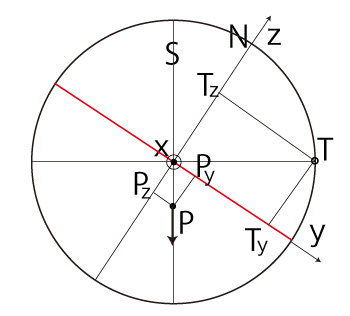
|
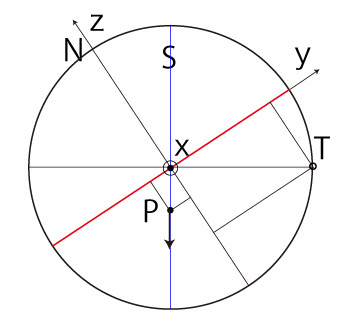
|
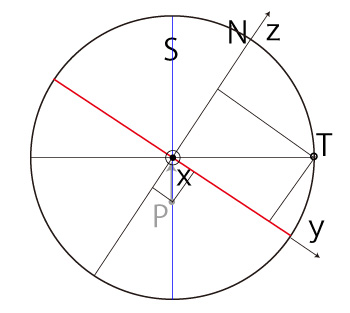
|
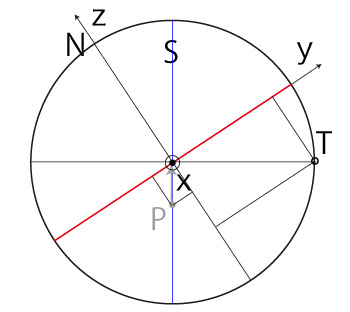
よって, \[ T_y = - R\ \frac{ P_z }{ \sqrt{ R^2 - P_x^2 } } \\ T_z = R\ \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\ \] |