\( (P, {\bf{ v }}) \)-回転角 \( \alpha \)
\[
- \pi < \alpha \leqq \pi
\]
をつぎのように定義する:
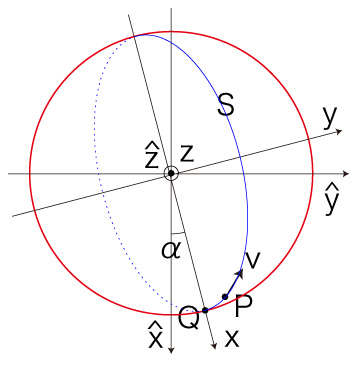
\( \alpha \) は, \( P,\ {\bf{ v }} \) の固定座標
\[
P = ( P_{\hat{x}},\ P_{\hat{y}},\ P_{\hat{z}} ) \\
{\bf{ v }} = ( v_{\hat{x}},\ v_{\hat{y}},\ v_{\hat{z}} )
\]
で表される。
以下,これを示す。
\( Q \) の座標 \( ( Q_{\hat{x}},\ Q_{\hat{y}},\ Q_{\hat{z}} ) \) は:
\( P_z = 0 \) のとき
\[
Q_{\hat{x}} = P_{\hat{x}} \\
Q_{\hat{y}} = P_{\hat{y}} \\
Q_{\hat{z}} = P_{\hat{z}} = 0 \\
\]
\( P_z > 0 \) のとき,
\[
Q_{\hat{x}} = - R\ \frac{ B }{ \sqrt{ A^2 + B^2 } } \\
Q_{\hat{y}} = R\ \frac{ A }{ \sqrt{ A^2 + B^2 } } \\
\]
\( P_z < 0 \) のとき,
\[
Q_{\hat{x}} = R\ \frac{ B }{ \sqrt{ A^2 + B^2 } } \\
Q_{\hat{y}} = - R\ \frac{ A }{ \sqrt{ A^2 + B^2 } } \\
\]
ここで
\[
\quad A = P_{\hat{x}}^2\ v_{\hat{y}} - P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{x}} - R^2\ v_{\hat{y}} \\
\quad B = P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{y}} - P_{\hat{y}}^2\ v_{\hat{x}} + R^2\ v_{\hat{x}} \\
\]
\( P_z = 0 \) のときは,つぎのようになる:
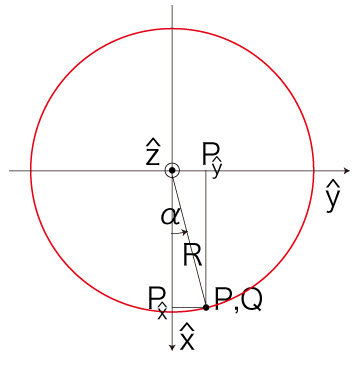
よって,
\[
R\ sin( \alpha ) = Q_{\hat{y}} = P_{\hat{y}} \\
\]
そして \( - \pi < \alpha \leqq \pi \) なので,
\[
\alpha = sin^{-1} \bigl( \frac{ P_{\hat{y}} }{ R } \bigr) \\
\]
\( P_z > 0 \) のときは,
\[
R\ sin( \alpha ) = Q_{\hat{y}} = R\ \frac{ A }{ \sqrt{ A^2 + B^2 } } \\
\]
そして \( - \pi < \alpha \leqq \pi \) なので,
\[
\alpha = sin^{-1} \bigl( \frac{ A }{ \sqrt{ A^2 + B^2 } } \bigr) \\
\]
\( P_z < 0 \) のときは,
\[
R\ sin( \alpha ) = Q_{\hat{y}}= - R\ \frac{ A }{ \sqrt{ A^2 + B^2 } } \\
\]
そして \( - \pi < \alpha \leqq \pi \) なので,
\[
\alpha = sin^{-1} \bigl( - \frac{ A }{ \sqrt{ A^2 + B^2 } } \bigr) = - sin^{-1} \bigl( \frac{ A }{ \sqrt{ A^2 + B^2 } } \bigr) \\
\]
まとめ
\[
P_z = 0 \Longrightarrow \ \alpha = sin^{-1} \bigl( \frac{ P_{\hat{y}} }{ R } \bigr) \\
\ \\
P_z > 0 \Longrightarrow \ \alpha = sin^{-1} \bigl( \frac{ A }{ \sqrt{ A^2 + B^2 } } \bigr) \\
P_z < 0 \Longrightarrow \ \alpha = - sin^{-1} \bigl( \frac{ A }{ \sqrt{ A^2 + B^2 } } \bigr)
\]
ここで
\[
\quad A = P_{\hat{x}}^2\ v_{\hat{y}} - P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{x}} - R^2\ v_{\hat{y}} \\
\quad B = P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{y}} - P_{\hat{y}}^2\ v_{\hat{x}} + R^2\ v_{\hat{x}} \\
\]
|



