一般に,直交座標軸をz軸を回転軸にして角度θ回転したときの同一点の座標の変化
\[
( A_x,\ A_y,\ A_{\hat{z}} ) \longrightarrow ( A'_x,\ A'_y,\ A'_{\hat{z}} )
\]
は,正規直交基底の座標の変化が
\[
( 1,\ 0,\ 0 ) \longrightarrow \ ( cos( \theta ),\ - sin( \theta ),\ 0 ) \\
( 0,\ 1,\ 0 ) \longrightarrow \ ( sin( \theta ),\ cos( \theta ),\ 0 ) \\
( 0,\ 0,\ 1 ) \longrightarrow \ ( 0,\ 0,\ 1 ) \\
\]
なので,つぎの座標変換式に表される:
\[
( A'_x,\ A'_y,\ A'_{\hat{z}} )
= ( A_x,\ A_y,\ A_z )
\left(
\begin{array}{ccc}
cos( \theta ) & - sin( \theta ) & 0 \\
sin( \theta ) & cos( \theta ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\]
よって,同じ点を指す固定座標 \( ( \hat{A}_x,\ \hat{A}_y,\ \hat{A}_z ) \) と \( (P, {\bf{ v }}) \)-座標 \( ( A_x,\ A_y,\ A_z ) \) の変換式は:
\[
\begin{align}
( A_x,\ A_y,\ A_z )
&= \ ( \hat{A}_x,\ \hat{A}_y,\ \hat{A}_z )
\left(
\begin{array}{ccc}
cos( \alpha ) & - sin( \alpha ) & 0 \\
sin( \alpha ) & cos( \alpha ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\ \\ \ \\
( \hat{A}_x,\ \hat{A}_y,\ \hat{A}_z )
&= ( A_x,\ A_y,\ A_z )
\left(
\begin{array}{ccc}
cos( - \alpha ) & - sin( - \alpha ) & 0 \\
sin( - \alpha ) & cos( - \alpha ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\\
&= ( A_x,\ A_y,\ A_z )
\left(
\begin{array}{ccc}
cos( \alpha ) & sin( \alpha ) & 0 \\
- sin( \alpha ) & cos( \alpha ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\end{align}
\]
同じ速度ベクトルを指す固定座標 \( ( u_\hat{x},\ u_\hat{y},\ u_\hat{z}, ) \) と \( (P, {\bf{ v }}) \)-座標 \( ( u_x,\ u_y,\ u_z ) \) の変換は,どうなるか?
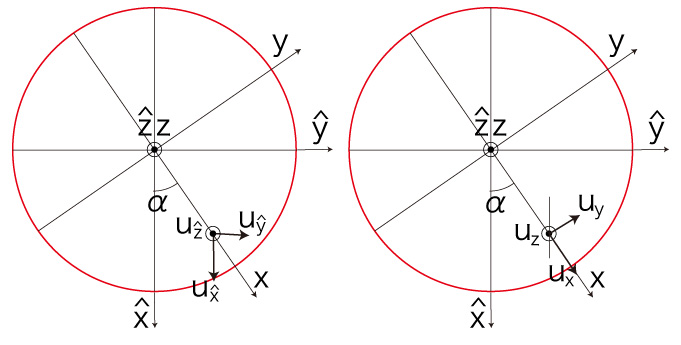
上の図から,\( ( u_\hat{x},\ u_\hat{y},\ u_\hat{z} ) \longrightarrow ( u_x,\ u_y,\ u_z ) \) では
\[
u_x = u_\hat{x}\ cos( \alpha ) + u_\hat{y}\ sin( \alpha ) \\
u_y = - u_\hat{x}\ sin( \alpha ) + u_\hat{y}\ cos( \alpha ) \\
u_z = u_\hat{z} \\
\]
そして \( ( u_x,\ u_y,\ u_z ) \longrightarrow ( u_\hat{x},\ u_\hat{y},\ u_\hat{z} ) \) では
\[
u_\hat{x} = u_x\ cos( \alpha ) - u_y\ sin( \alpha ) \\
u_\hat{y} = u_x\ sin( \alpha ) + u_y\ cos( \alpha ) \\
u_\hat{z} = u_z \\
\]
<行列の作用>の形に表現すると:
\[
( u_x,\ u_y,\ u_z )
= ( u_\hat{x},\ u_\hat{y},\ u_\hat{z} )
\left(
\begin{array}{ccc}
cos( \alpha ) & - sin( \alpha ) & 0 \\
sin( \alpha ) & cos( \alpha ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\\
\ \\ \ \\
( u_\hat{x},\ u_\hat{y},\ u_\hat{z} )
= ( u_x,\ u_y,\ u_z )
\left(
\begin{array}{ccc}
cos( \alpha ) & sin( \alpha ) & 0 \\
- sin( \alpha ) & cos( \alpha ) & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\]
|
