- 「系列」としての自然数は,「ペアノ (Peano)(註))の公理」という形で数学的に定義されます。
自然数の系は,先ず,集合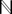 と, と,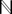 の一つの要素1と,関数f: の一つの要素1と,関数f: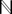 ─→ ─→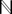 の組
( の組
(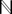 ,1,f) ,1,f)
であり,そしてこれについて,以下のことが成立している:
1° f(x)=1となる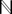 の要素xは存在しない; の要素xは存在しない;
2° 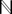 の要素x,yについてf(x)=f(y)ならばx=y; の要素x,yについてf(x)=f(y)ならばx=y;
3° 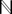 の部分集合 の部分集合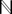 ′は,つぎの条件を満たすとき,実は ′は,つぎの条件を満たすとき,実は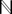 と一致している: と一致している:
1が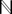 ′の要素になっている; ′の要素になっている;
xが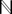 ′の要素のとき,f(x)も ′の要素のとき,f(x)も ′の要素. ′の要素.
|
- どうしてこれが「系列」の定義 (数学化) になっているのか,ちょっと見にはわかりません:
(註) Peano,G.:1858-1932
|