→ 八元数 → 十六進数 どうしてこうなるかというと,新しい「数」をつくっていくやり方が,「直近の改造」だからである。 隣り同士は似ているが,隔たるにしたがい別物になっていく。 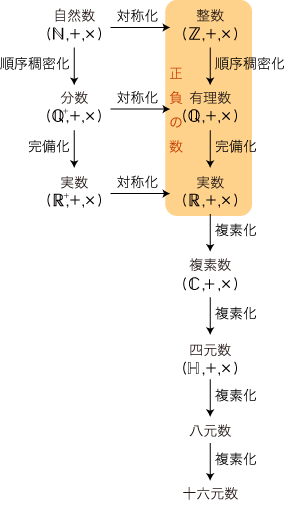
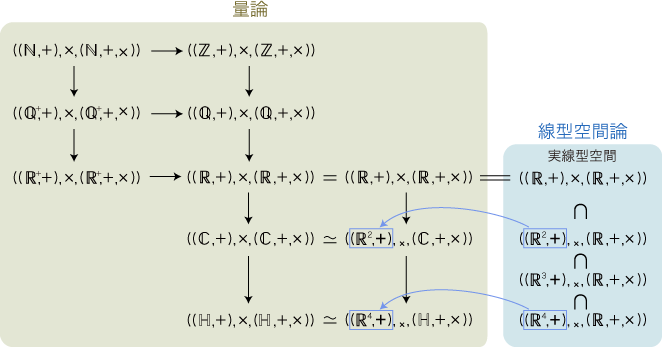
数学は,実数,複素数,四元数から定義される量形式
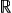 , +), ×, ( , +), ×, (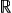 , +, ×) ) , +, ×) )
( ( 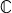 , +), ×, ( , +), ×, (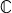 , +, ×) ) , +, ×) )
( (  , +), ×, ( , +), ×, ( , +, ×) ) , +, ×) )
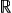 , +), ×, ( , +), ×, (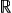 , +, ×) ) , +, ×) )
( ( 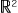 , +), ×, ( , +), ×, (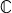 , +, ×) ) , +, ×) )
( ( 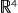 , +), ×, ( , +), ×, ( , +, ×) ) , +, ×) )
これらは,線型空間論の実線型空間から材料をとってきている。 特に,( ( 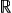 , +), ×, ( , +), ×, (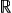 , +, ×) ) は,「量」と「線型空間」の両方の見方ができる。 , +, ×) ) は,「量」と「線型空間」の両方の見方ができる。
|