Up 十進数の延長  

    分数と小数が対象とする量は，ともに順序稠密量ということで，同じである。 しかし，日常生活では小数がもっぱら使われる。 それは，小数が十進数の延長になるからである。

    分数が自然数を直接ベースにするのに対し，小数は十進数をベースにする。 《自然数そのものではなく，自然数実現の一形態であるところの十進数が，小数のベースになる》──このとらえが重要である。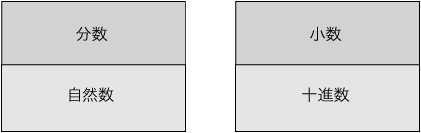
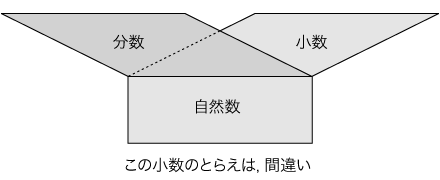
    実際，このとらえを失すると，自然数の上に分数と小数が横並びした図を描くふうになってしまう。

    「十進数」とは何か？

    自然数の出自は，個数（離散量）の対象化である。 個数を表現しようとする実践の中から，自然数(「系列」)がつくられてくる。
    「系列」の数学的定式化は，ペアノの公理である。

    「系列」の実現の仕方は，一通りではない。
    「系列」の実現方法として，「十進数」が考え出された。
    十進数の「十」は，人の指の本数が十であることに拠る。 指で数える行為が，自ずと「十進」を導いたのである。 数としての特別な意味が「十」にあるわけではない。


    わたしたちにとって，「十進数」は自然数としてあたりまえのものになっている。 すなわち，十進数と自然数の混同が普通になっている。
    実際，自然数と十進数を区別できるようにするものは，数学である。 翻って，自然数と十進数の混同のあるところには，数学の閑却がある。