Up 「比例」の数学 作成: 2013-11-20
更新: 2013-11-30

    「比例」は，「２量の間の比例関係」のことであり，これはつぎの言い回しで定義される：
      「２量の間の対応関係で，
      　一方の２倍，３倍，‥‥に他方の２倍，３倍，‥‥が対応する」

    この定義は，一見，有理数倍および実数倍を欠く不完全な定義に見える。
    しかし実際には，有理数および実数○に対する「一方の○倍に他方の○倍が対応」がこの定義から導かれるので，定義として問題ない ( 証明は数の拡張に乗せていくものである → 証明)。

    いま，ｆ：量1 → 量2 を比例関係とする。
    「一方の○倍に他方の○倍が対応」は，式で書くとつぎのようになる：
      ｆ(ｑ × ｎ) ＝ ｆ(ｑ) × ｎ　 (ｑ ∈ 量1，ｎ：数)


    つぎのステージは，量1，量2 それぞれにおいて，単位 ｕ1，ｕ2 を固定することから開始される。

    量1 の任意の要素ｑ1 は，ｕ1 の何倍の形に書ける：
      ｑ1 ＝ ｕ1 × ｎ1
    これを，つぎのように言っているわけである：
      「単位ｕ1 に対するｑ1 の(測定)値は，ｎ1 」

    量2 の場合も同様である。
    そこで，ｆ：量1 → 量2 からは，数値の対応が導ける。
    この対応をφ(ファイ) とする：
      φ：数 → 数

    さて，ｆには「一方の○倍に他方の○倍が対応」のきまりがある。
    そこで，「ｆから導かれるφにも何かきまりが見出されるはずだ」と考えるのは，自然である。
    そして，きまりを求めてみると，「一定数倍」が求まる：
      φ：ｎ├─→ ｎ × ａ
    ａは，ｆ(ｕ1) ＝ ｆ(ｕ2) × ａ となる数である。
    これが，学校数学の「ｙ＝ａｘ」であり，ａを「比例定数」と呼ぶ。

    「ｙ＝ａｘ」の要点は，つぎの２つである：
    1. 「ｙ＝ａｘ」は，数と数の間の対応
      　（「比例関係」は，量と量の間の対応）
    2. 「比例定数」ａは，２量での単位の取り方に依存


    そして，以上の内容は「線型空間」の数学と対比できるものになる：
    1. 「量」は，「線型空間」と対応
    2. 「比例関係：量1 → 量2 」は，「線型写像：線型空間1 → 線型空間2 」と対応
    3. 「単位ｕ」は，「基底Ｕ＝ (ｕ1, ‥‥, ｕｎ )」と対応
    4. 「単位ｕ に対する量ｑ の(測定)値」は，「基底Ｕに対するベクトルｖ の座標」と対応
    5. 「量1 の単位 ｕ1，量2 の単位ｕ2 に対し比例関係ｆ：量1 → 量2 から導かれる比例定数」は， 「線型空間1 の基底Ｕ1，線型空間2 の基底Ｕ2 に対し線型写像ｆ：線型空間1 → 線型空間2 から導かれる行列 (「ｆの表現行列」)」と対応

    実際，この対比は，実数係数の「量」と「１次元線型空間」が同じものになることに因っている。
    （そして実数係数では，「比例定数ａ」は「１×１行列 (ａ)」と同じ！）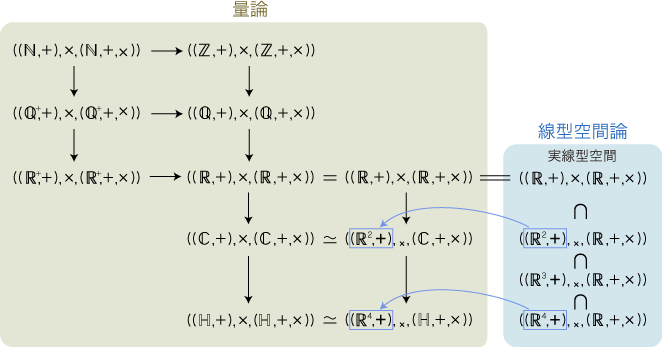




    「一方の２倍，３倍，‥‥に他方の２倍，３倍，‥‥が対応する」から，整数，有理数，実数係数での「一方の○倍に他方の○倍が対応」が導かれることの証明：
    先ず，つぎのことに留意する ( 『「数とは何か？」への答え』)：
      量の系 ( ( Ｑ, ＋ ), ×, ( Ｎ, ＋, × ) ) は，( ( Ｎ, ＋ ), ×, ( Ｎ, ＋, × ) ) と同型に立てられる。
      即ち，Ｑ は０でないｕ∈Ｑに対する｛ ｕ×ｎ｜ｎ∈Ｎ｝の形になり，つぎの対応が ( ( Ｎ, ＋ ), ×, ( Ｎ, ＋, × ) ) と ( ( Ｑ, ＋ ), ×, ( Ｎ, ＋, × ) ) の間の同型になる：
        ｎ├─→ ｕ×ｎ (ｎ∈Ｎ)

    Ｎが負数をもつ数 ( e.g. ，， ) の場合，各ｑ∈ Ｑ には対称元 ーｑがある。さらに，つぎが成り立つ：
      ｑ × ｎ＝ (ーｑ )× (ーｎ)

      証明：
      ｑ＝ｕ × ａとする。
      ｑ × ｎ＝ｕ × (ａ×ｎ)。
      ａ×ｎと ー(ａ×ｎ) は，互いに対称元。 そこで，ｕ × (ａ×ｎ) とｕ × (ー(ａ×ｎ)) は，対称元。
      また，ｕ × (ー(ａ×ｎ)) と (−ｕ) × (ー(ａ×ｎ)) は，足して０になるので，対称元。
      そして，
        (ーｕ) × (ー(ａ×ｎ)) ＝ ((ーｕ) ×ａ) × (ーｎ) ＝ (ー(ｕ ×ａ)) × (ーｎ) ＝ (ーｑ) × (ーｎ)
      結局，ｑ × ｎ＝ (ーｑ )× (ーｎ)

    量の系 ( ( Ｑ1, ＋ ), ×, ( Ｎ, ＋, × ) )， ( ( Ｑ2, ＋ ), ×, ( Ｎ, ＋, × ) ) と関数 ｆ：Ｑ1 → Ｑ2 において，つぎが成り立っているとする：
      ｆ(ｑ × ｎ) ＝ ｆ(ｑ) × ｎ　（ｎ＝ 2, 3, ‥‥ )
    但し，Ｎが０をもつ数のときは，つぎを条件にする：
    1. ｆ(ｑ × ｎ) ＝ ｆ(ｑ) × ｎ　（ｎ＝ 0, 1, 2, 3, ‥‥)
    2. (「非退化」)
      ｆ(０) ＝ ０，かつｆ(ｑ) ＝ ０ となるｑは０に限る。

    つぎが成り立つ：
    1. ｆは１対１
    2. ｆ(ーｑ) ＝ ーｆ(ｑ)

      証明：
      1. ｆ(ｑ) ＝ ｆ(ｑ′) とする。
        ｑ ＝ｕ×ａ，ｑ′ ＝ｕ×ａ′ とすると，
          　ｆ(ｑ) ×ａ′
          ＝ｆ(ｕ×ａ) ×ａ′
          ＝ｆ(ｕ) × (ａ×ａ′ )
          ＝ｆ(ｕ×ａ′ ) ×ａ
          ＝ｆ(ｑ′) ×ａ
          ＝ｆ(ｑ) ×ａ
        よって，ａ′ ＝ａ。
        結局，ｑ ＝ｑ′。
      2. ｆ(ーｑ) ＝ ｆ(ｑ) ×ｎ とする。
        ｆ(ーｑ) ＝ ｆ(ｑ) ×ｎ ＝ｆ(ｑ×ｎ) より，ーｑ＝ｑ×ｎ。
        よってｎ＝ー1。
        ｆ(ーｑ) ＝ ｆ(ｑ) ×ｎ ＝ ｆ(ｑ) × (ー1) ＝ ーｆ(ｑ)。

    以上の準備のもと，これより本題の証明に入る。

    (1) Ｎが整数の場合
    　ｆ(ｑ × (ー２)) ＝ｆ(ｑ) × (ー２) を示す：
      　 ｆ(ｑ × (ー２))
      ＝ ｆ((ーｑ) × ２)
      ＝ ｆ(ーｑ) × ２
      ＝ (ーｆ(ｑ)) × ２
      ＝ ｆ(ｑ) × (ー２)

    (2) Ｎが分数 (正の有理数) の場合
    　ｆ(ｑ × 2/3) ＝ｆ(ｑ) × 2/3 を示す：
      ｑ × 2/3 ＝ｑ′ とする。
      これは，つぎの条件を満たすｃ∈Ｑ1 が存在するということ：
        ｃ × 3 ＝ｑ
        ｃ × 2 ＝ｑ′
      「Ｎが自然数の場合」に還って，
        ｆ(ｃ) × 3 ＝ｆ(ｃ × 3) ＝ｆ(ｑ)
        ｆ(ｃ) × 2 ＝ｆ(ｃ × 2) ＝ｆ(ｑ′)
      そしてこれは，ｆ(ｑ) × 2/3 ＝ｆ(ｑ′) ということ。

    (3) Ｎが実数の場合
    　ｆ(ｑ × π) ＝ｆ(ｑ) × π を示す：
      ｛ｎk｜k＝1,2,‥‥｝を，πを定める有理数の Cauchy列とする。
      先ず，｛ｑ ×ｎk｜k＝1,2,‥‥｝が，Ｑ1 における Cauchy列になり，これより｛ｆ(ｑ ×ｎk)｜k＝1,2,‥‥｝が，Ｑ2 における Cauchy列になる。 そして，これが定めるＱ2 の要素はｆ(ｑ ×π)。
      また，Cauchy列｛ｆ(ｑ ×ｎk)｜k＝1,2,‥‥｝は，「Ｎが有理数の場合」に還って，｛ｆ(ｑ) ×ｎk｜k＝1,2,‥‥｝であり，そして，｛ｆ(ｑ) ×ｎk｜k＝1,2,‥‥｝が定めるＱ2 の要素はｆ(ｑ) ×π。
      よって，ｆ(ｑ × π) ＝ｆ(ｑ) × π。