中学生なら,「何」を求めるのにつぎの式を立てる:
しかし,どうしてこの式になるのか? この立式の論理を,ここで確認する。 このときの<世界>は,つぎのもので構成されている:
これの数学は「線型空間・アフィン空間」で,つぎのように対応する:
f とFは,それぞれつぎのように条件付けられる関数である: 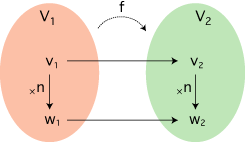
F(P + v) = F(P) + f(v) 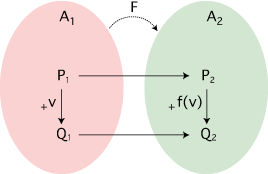
そして,以上のことを使って,つぎの計算になる:
=F(T時 + x時間) =F(T時) + f(x時間) =F(T時) + f(時間 × x) =(基準点からbkm) + ( f(時間) × x) ) =(基準点 + ( km × b ) ) + ( (km × a) × x) =(基準点 + ( km × b ) ) + ( km × (a×x) ) =基準点 + ( ( km × b ) +( km × (a×x) ) ) =基準点 + ( km × ( b + (a×x) ) ) 特に,「b + (a×x)」──すなわち,「ax+b」──が数計算ということになる。 以上の推論は,すぐれて数学である。 一方,問題に対して「ax+b」を立式することは,この数学を知らない/理解できない小・中学生にもできる。 「わからなくてもできる」ということである。
では,どうして「できる」のか? パターンのとらえと「このパターンに対してはこのようにする」をやっているのである。 |