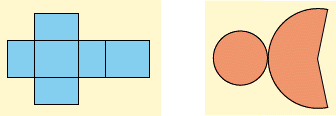- 「部品 (パーツ) の貼り合わせ」も,モノに対する幾何学的な見方のうちの一つです。
- 以下は,「パーツへの展開,パーツの貼り合わせ」の例です:
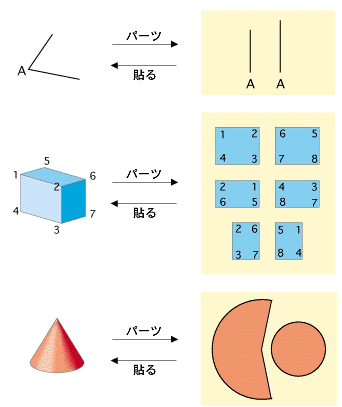
- パーツへの展開,パーツの貼り合わせでは,「素材変形の自由度」が暗黙に考えられています。
- 箱の形の展開図に折りしろを設けるときは,「折る」ができる素材を想定しています。
例えば紙であり,プラスチックではありません。
- 円錐の展開図やつぎの発展問題1では,「曲げる」ができる素材を想定しています。
例えば紙であり,プラスチックではありません。
- つぎの発展問題2では,「伸縮自在」を考えられる素材を想定しています。例えばゴム膜であり,紙ではありません。
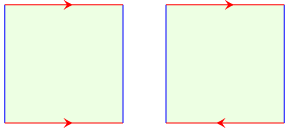
- 発展問題1:つぎの「貼り合わせ」では,どんな形ができるでしょう?
(同じ色の辺を,矢線の方向が一致するように貼ってください)
 こたえ こたえ
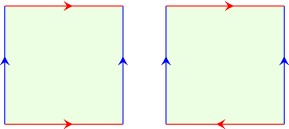
- 発展問題2:つぎの「貼り合わせ」では,どんな形ができるでしょう?
(同じ色の辺を,矢線の方向が一致するように貼ってください)
 こたえ こたえ
- 「展開図」の主題は,つぎの場合の「パーツへの展開,パーツの貼り合わせ」です:
- 「展開図」を,全体で一つにつながっているものと思いこんでいる人が(教員の中にも)います。
「つながっている」ことを肝心なことのように考え,つぎのようなのを「展開図」とみなしているわけです:
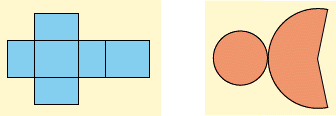
このような思い込みは,もちろん誤りです。
特に,「折り目」は「展開図」の本質的な要素ではありません。それは「貼り合わせ」の中途段階というべきです。
実際,紙を素材にして展開図を考えるから「折り目」にしてしまうのです。
プラスチック板を素材にしたとき,「折り目」を書きますか?そうはしないでしょう。プラモデルのように要素をバラバラにして,ノリシロを指示する方法をとるはずです。
- 展開図の応用
- 立体の表面上の2点間の最短距離を求める──この最短距離を示す線分を求める。
- 発展問題1 のこたえ
- 発展問題2 のこたえ
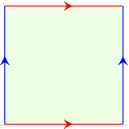 |
──→ |
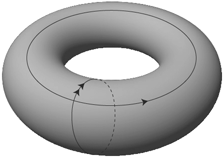
「トーラス (torus)」 |
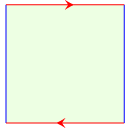 |
──→ |
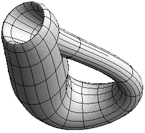
「クラインの壺 (Klein's bottle)」
(画像は Mathematica で作成)
|
|
 「展開図」の指導
「展開図」の指導



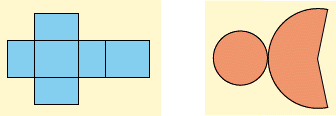
 「展開図」の指導
「展開図」の指導