\( Ker( \partial_1 ) / Im( \partial_2 ) \) の基底の導出手順を,以下に記す。
これは,概観である。
ここまで本テクストを読み進めてきた読者は,「けっこうやることあるなあ」くらいに受け取ってくれたらよい。
──理解しようとする必要はない。
逆に,これまでに「ホモロジー群」に触れた経験のある読者は,「ホモロジー群の計算」の意味/内容に対する自分の理解があっているかどうかを,ここでチェックしてみるとよい。
\( Ker( \partial_1 ) / Im( \partial_2 ) \) の基底の導出は,つぎをすることである:
「\( Im( \partial_2 ) \) の基底を \( Ker( \partial_1 ) \) の基底の部分にし,そしてこれを潰す」
手順は,つぎのようになる:
- \( Ker( \partial_1 ),Im( \partial_2 ) \) の基底を求める。
──これは別々に求めることになる。
- 求めたら,\( Ker( \partial_1 ) \) の基底の各要素に対し,それが \( Im( \partial_2 ) \) の基底の線形結合に表せるかどうかを調べる。
この作業により,\( Im( \partial_2 ) \) の基底が \( Ker( \partial_1 ) \) の基底の部分になる。
- \( Ker( \partial_1 ) \) の基底の要素で \( Im( \partial_2 ) \) の基底の線形結合で表せなかったものを,同値関係「 \( mod\ Im( \partial_2 ) \)」で類別する。
── \( Ker( \partial_1 ) \) の要素 \( c_1, c_2 \) は,\( c_1 - c_2 \) が \( Im( \partial_2 ) \) の基底の線形結合に表せたら,同値。
- 得られた同値類が,\( Ker( \partial_1 ) / Im( \partial_2 ) \) の基底である。
\( Ker( \partial_1 ),Im( \partial_2 ) \) の基底を求める方法は,
- \( \partial_1, \partial_2 \) を行列に表現する。
- その行列に対し,「行列の階数を求める計算」を施す。
\( \partial_1 \) の表現行列の場合は:
- 「行列の階数を求める計算」で潰れる次元が,\( Ker( \partial_1 ) \) の次元になる。
- このときの「行列の階数を求める計算」のプロセスを追うことで,「潰れる次元」の内容になった \( C_1 \) の要素が求まる。
この要素が,\( Ker( \partial_1 ) \) の基底になる。
\( \partial_2 \) の表現行列の場合は:
- 「行列の階数を求める計算」で潰れなかった次元が,\( Im( \partial_2 ) \) の次元になる。
- このときの「行列の階数を求める計算」のプロセスを追うことで,「潰れなかった次元」の内容になった \( C_1 \) の要素が求まる。
この要素が,\( Im( \partial_2 ) \) の基底になる。
「表現行列」は「始空間のこの基底と終空間のこの基底に対する表現行列」である。
\( \partial_1, \partial_2 \) の行列表現は,\( C_0, C_1, C_2 \) の基底を固定することが,最初の作業になる。
この作業は,「向きを定める」と言い表されている。
\( Ker( \partial_1 ) \) の基底の各要素に対し,それが \( Im( \partial_2 ) \) の基底の線形結合に表せるかどうかを調べるのは,泥臭い作業である。
\( Ker( \partial_1 ) \) の基底の要素で \( Im( \partial_2 ) \) の基底の線形結合で表せなかったものを,同値関係「 \( mod\ Im( \partial_2 ) \)」で類別するのも,泥臭い作業である。
ともに泥臭い作業であると,観念すべし。
「向きを定める」を \( C_1 \) の場合で簡単に説明すると:
「一つの辺が現す二つの有向辺のうち,一方を基底の要素として固定」
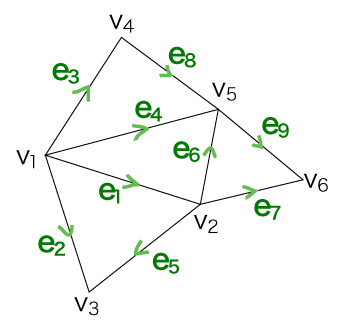
このとき,\( e_i = \overrightarrow{v_j v_k}\ \) の逆 \( \ \overrightarrow{v_k v_j}\ \) は \( - e_i \) となる。
基底 \( { e_i } \) を使ったチェインの表現の例:
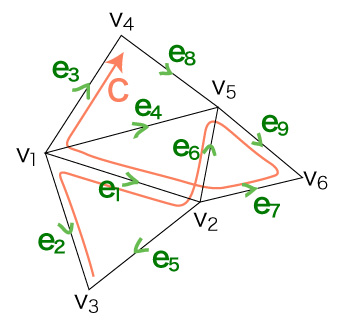
|
\[
\begin{align}
c &= ( - e_2 ) + e_1 + e_6 + e_9 + ( - e_7 ) + ( - e_1 ) + e_3 \\
&= ( ( - e_2 ) + e_3 ) + ( e_1 + ( - e_1 ) ) + ( e_6 + e_9 + ( - e_7 ) ) \\
&= ( ( - e_2 ) + e_3 ) + ( e_6 + e_9 + ( - e_7 ) ) \\
\end{align}
\]
|
|



 トーラス : \( C_1, C_2 \) の基底を定める (「向きを定める」)
トーラス : \( C_1, C_2 \) の基底を定める (「向きを定める」)