Up ホモロジー加群 \( H_1 = Ker( \partial_1 ) / Im( \partial_2 ) \) 作成: 2023-10-11
更新: 2023-10-14

    トーラスには，球面には無い周回のタイプを見て取れる：
    \( a \) のタイプはどの閉曲面にもあり，これは「面の境界になっている」で特徴づけられる。

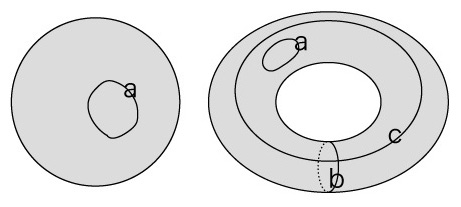
    われわれは，閉曲面を三角面複体に同相変換して，周回をサイクルに，\( a \) タイプの周回をバウンダリサイクルに表現した。
    こうして，「\( a \) タイプ以外のタイプ」は「バウンダリサイクルでないサイクル」の話になる。
    そしていま，「バウンダリサイクルでないサイクル」を捉える段にまでやって来た。


    サイクルは，バウンダリが０になるチェインである。
    よって，\( Ker( \partial_1 ) \) がこれを捉えていることになる。
    バウンダリサイクルは，面のバウンダリになるサイクルである。
    よって，\( Im( \partial_2 ) \) がこれを捉えていることになる。

    \( Ker( \partial_1 ), Im( \partial_2 ) \) は，\( \mathbb{Z} \)加群 \( C_1 \) の部分空間であり，\( Ker( \partial_1 )\ \supset\ Im( \partial_2 ) \) である。
    こうして，「バウンダリサイクルでないサイクルを捉える」は，「\( Ker( \partial_1 ) \) の中の \( Im( \partial_2 ) \) の補空間を捉える 」である。

    \( Ker( \partial_1 ) \) の中の \( Im( \partial_2 ) \) の補空間とは，\( Ker( \partial_1 ) \) の中で \( Im( \partial_2 ) \) の次元を潰したものである。
    イメージとして：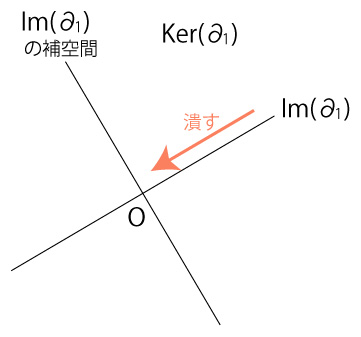
    「\( ( x, y ) \) 座標を \( y \) 座標に射影」の感じである。


    「\( Ker( \partial_1 ) \) の中で \( Im( \partial_2 ) \) の次元を潰す」は，\( Im( \partial_2 ) \) の基底が \( Ker( \partial_1 ) \) の基底の部分になっている場合である。
    ホモロジー加群を導入しこれの基底を求めることは，「\( Im( \partial_2 ) \) の基底を \( Ker( \partial_1 ) \) の基底の部分にし，そしてこれを潰す」と同じである。

    ホモロジー加群は，「商空間」で定義される：
      \[ H_1 = Ker( \partial_1 ) / Im( \partial_2 ) \]
    「\( Im( \partial_2 ) \) の基底を \( Ker( \partial_1 ) \) の基底の部分にし，そしてこれを潰す」を「商空間 \( Ker( \partial_1 ) / Im( \partial_2 ) \) の基底」の話にすることには，つぎのメリットがある：，
    • 「商空間」の方が概念として一般的であり，既存の商空間論を利用できる。
    • 「商空間」の方が，記述がラク。──推論を構造化しやすい。


    われわれがやろうとすることは，「ホモロジー加群の基底を求める」である。
    バウンダリサイクルでないサイクルのタイプは，ホモロジー加群の基底がこれを表すことになる。
    「バウンダリサイクルでないサイクルを捉える」は，つぎが結論の形になる：
      「タイプが○個あり，各タイプの代表元は ‥‥ 」