「長さ」では，(「３cmの長さ」のように) 個々の長さが考えられている。 この個々の長さ全体の集合を考え，Ｑで表す。 個々の長さはＱの要素ということになったので，これを「長さ(要素)」と言い表す。 一方，Ｑの方を「長さ(集合)」と言い表す。 ２つの長さ(要素) の間には，比が考えられている。 そして，この比の表現に用いることになるのが，数である。 長さに伴う数が ( N, ＋, × ) であるとしよう。
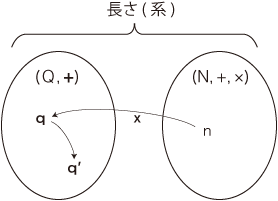
「比」の別表現に「倍」がある。 この二つの表現は，ｑ, ｑ' ∈ Ｑ と ｎ ∈ Ｎ に対するつぎの＜言い換え＞の関係にある：
ここまでで，長さは，長さ(集合) Ｑ と数 ( N, ＋, × ) と倍作用 × を構成要素とする系ということになった 。この系──「長さ(系)」──をつぎのように表すとしよう：
この加法を，記号「＋」で表す。
こうして，長さ(系) は，最終的につぎの構成になった：
以上「長さ」について，これの系としての構成を示した。 しかし，この構成を導いてきた論法は，他の量 (「重さ」「時間」「速さ」‥‥ ) でも同じになる。 そこで一般に，「量」が系，集合，要素のいずれを指すかでそれぞれ「量(系)」「量(集合)」「量(要素)」の言い回しを用いることにし，そしてつぎを量(系) の表現とする：
|
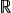を考えることになる。