特に,数のいろいろ(自然数,整数,有理数,‥‥)に量のいろいろが応じることになる。 こうして,量より先に数があることになり,「数」の意味 (定義) が問題になってくる。 「数」の意味を考えるために,実際にどんなものを「数」と呼んでいるかを,先ず押さえておこう。 現前の数(系) は,四元数までの構築の流れがつぎのようになっている: 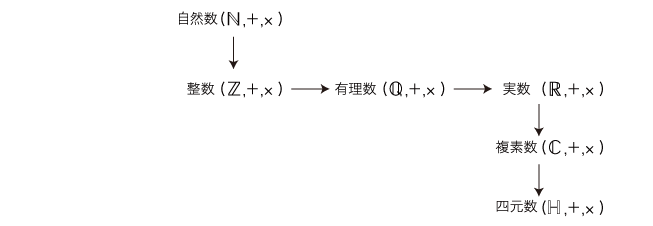 これらは,量(系) をつぎのカテゴリー区分で対象化するものになっている: 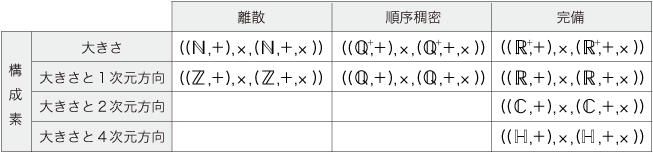
( ( 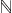 , +), ×, ( , +), ×, (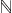 , +, ×) ) の離散と ( ( , +, ×) ) の離散と ( (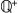 , +), ×, ( , +), ×, (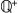 , +, ×) ) の順序稠密の違いは,前者では2量で比をもてないものが出てくるのに対し,後者ではどの2量も比が一意的に定まるという違いとも,相応じている。 , +, ×) ) の順序稠密の違いは,前者では2量で比をもてないものが出てくるのに対し,後者ではどの2量も比が一意的に定まるという違いとも,相応じている。
「大きさとn次元方向・完備」のカテゴリーの量 ( (Q, +), ×, (N, +, ×) ) として数学の中で実際に対象にされるものは,n次元実ベクトル空間を母体にして構成したつぎのものである: 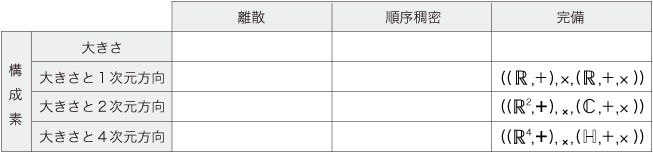
ここで, ( ( 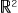 , +), ×, ( , +), ×, (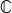 , +, ×) ) と ( ( , +, ×) ) と ( (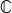 , +), ×, ( , +), ×, (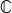 , +, ×) ) の同型: , +, ×) ) の同型: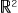 ─→ ─→ 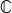 は,つぎの対応である: は,つぎの対応である:
また, ( ( 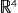 , +), ×, ( , +), ×, ( , +, ×) ) と ( ( , +, ×) ) と ( ( , +), ×, ( , +), ×, ( , +, ×) ) の同型: , +, ×) ) の同型: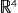 ─→ ─→  は,つぎの対応である: は,つぎの対応である:
複素数の実用性は,つぎの点にある:
それは複素数である。 四元数の実用性は,つぎの点にある:
それは四元数である。 ただし,「3次元実ベクトルの<比>になる数」をつくるとき,それは「4次元実ベクトルの<比>になる数」をつくることになって,そしてその数は四元数だということになる。 3次元実ベクトルは,4次元実ベクトル空間に埋め込むことで,四元数を<比>として用いられるようになる。
四元数になると,乗法が可換でなくなる。 ──これは,これは四元数の「数」としての著しい特徴になる。 (四元数については,つぎのテクストにあたられたい:『四元数』) |