- 線型写像の合成は,以下述べるように,表現行列の積の計算によって求めることができます。そしてこのときの行列の積は,比例定数の積とつぎのように対応しています:
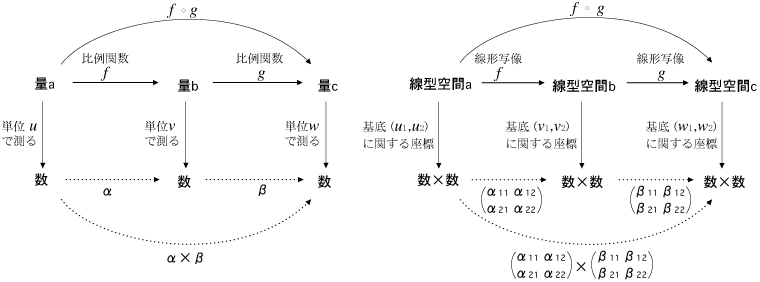
- 表現行列の積
- 線型写像f:Q ─→ Q',g:Q' ─→ Q" の合成 gf は,線型写像になります:
(gf)(x×ξ)=g(f(x×ξ))=g(f(x)×ξ)=g(f(x))×ξ=(gf)(x)×ξ
(gf)(x+y)=g(f(x+y))=g(f(x)+f(y))=g(f(x))+g(f(y))=(gf)(x)+(gf)(y)
|
- Qの基底(u1, u2),Q'の基底(v1, v2),Q"の基底(w1, w2) に対し,(u1, u2), (v1, v2) に関するfの表現行列を
| A= |
 |
α11 α12
α21 α22
|
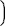 |
(v1, v2), (w1, w2) に関するgの表現行列を
| B=
|  |
β11 β12
β21 β22
|
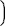 |
とするとき,(u1, u2), (w1, w2)に関するgfの表現行列を,AとBの積
A×B
の形で表すことにします。比例関数の合成に比例定数の積が対応しましたが,これに倣うわけです。
- A×Bの表す行列
 |
γ11 γ12
γ21 γ22
|
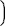 |
γij=αi1×β1j+αi2×β2j (i,j=1,2)
 |
α11 α12
α21 α22
|
 |
× |
 |
β11 β12
β21 β22
|
 |
= |
 |
α11×β11+α12×β21 α11×β12+α12×β22
α21×β11+α22×β21 α21×β12+α22×β22
|
 |
(註) 実際,
(gf)(ui)
=g(f(ui))
=g(v1×αi1+v2×αi2)
=g(v1×αi1)+g(v2×αi2)
=g(v1)×αi1+g(v2)×αi2
=(w1×β11+w2×β12)×αi1+(w1×β21+w2×β22)×αi2
=w1×(β11×αi1+β21×αi2)+w2×(β12×αi1+β22×αi2)
=w1×(αi1×β11+αi2×β21)+w2×(αi1×β12+αi2×β22)
したがって,
γi1=αi1×β11+αi2×β21
γi2=αi1×β12+αi2×β22
すなわち
γij=αi1×β1j+αi2×β2j (j=1,2)
|

