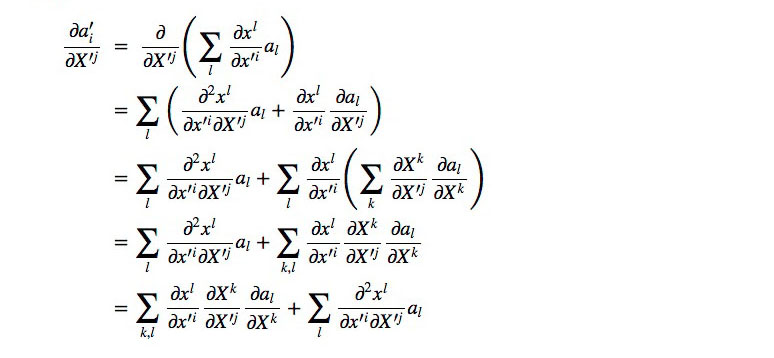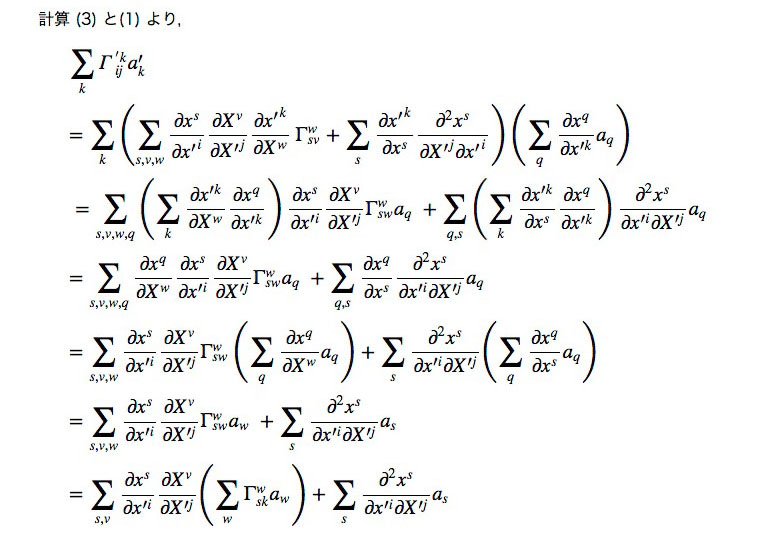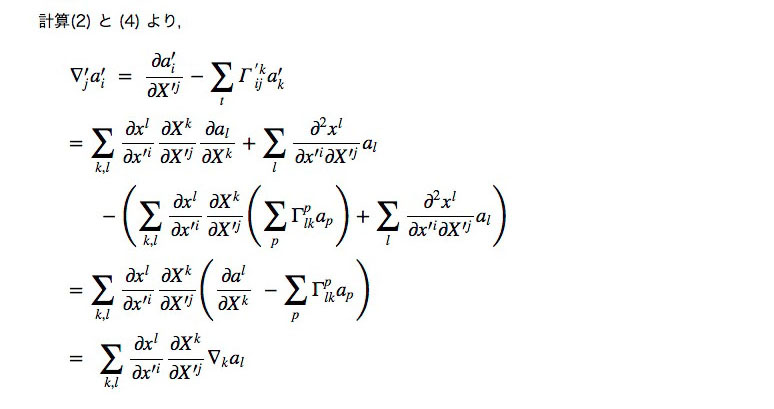\( {\nabla}_j a_i({\bf x})\) をつぎのように定義し,これを「共変微分」と呼ぶとした:
\[
{\nabla}_j a_i({\bf x}) = \frac{\partial a_i({\bf x}) } {\partial X^j}
+ \sum_k \Gamma^k_{ij}\, a_k({\bf x})
\]
「共変」の語は,この形式が基底変換に対して共変だということを示していることになる。
実際,つぎが成り立つ:
\[
\begin{align*}
\nabla'_j a'_i
\ =\ \frac{\partial a'_i}{\partial X'^j} - \sum_k {\it \Gamma}^{\,'k}_{\ ij} a'_k \\
=\ \sum_{k,l} \frac{\partial x^l}{\partial x'^i} \frac{\partial X^k}{\partial X'^j} \nabla_k a_l
\end{align*}
\]
以下,これの計算過程を示す。
計算(1)
\[
a'_i = \sum_j \frac{\partial x^j}{\partial {x'}^i}\, a_j
\]
(  「共変座標」) 「共変座標」)
計算(2)
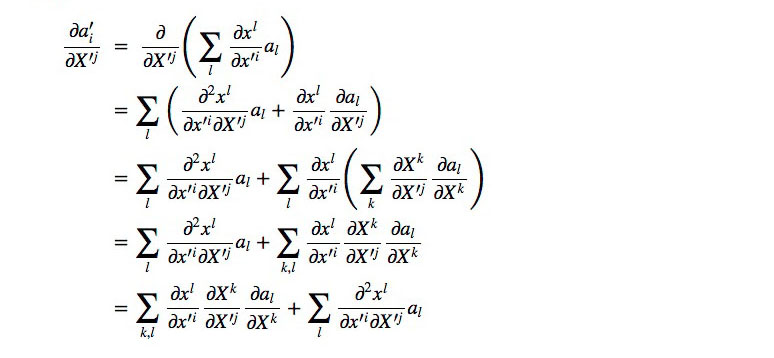
計算(3)

計算(4)
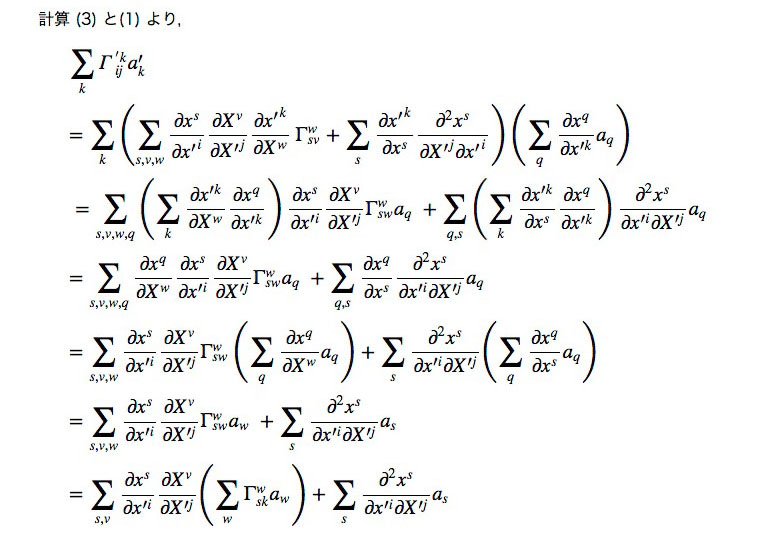
計算(5)
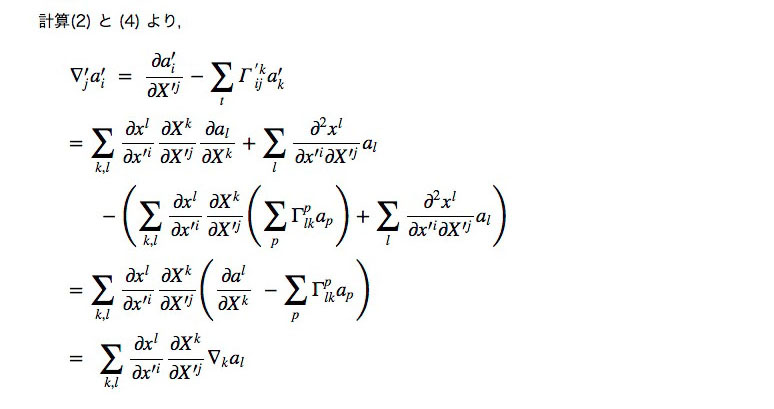
|
 「共変座標」)
「共変座標」)