「曲率」導出のアイデアを,実行に移すとする。
定義しようとするのは,リーマン多様体 M の「点 \(P\) における曲率」である。
「リーマン多様体」のテクストには,つぎの方法が書かれている:
- つぎのように設定する:
\(P \to Q \quad ( + d{\bf x}) \)
\( \phi_P \) を開き,ベクトル \( \bf A \) を \(P\) に置く。
\( \bf A \) を \(Q\) まで平行移動。
\(Q \to R \quad (+ d{\bf y}) \)
\( \phi_Q \) を開き,\( \phi_P \) を読み込む。
\( \bf A \) の像を,\( {\bf a}(Q) \) とする。
\( {\bf a}(Q) \) を \(R\) まで平行移動。
\(R \to S \quad ( - d{\bf x}) \)
\( \phi_R \) を開き,\( \phi_Q \) を読み込む。
\( {\bf a}(Q) \) の像を,\( {\bf a}(R) \) とする。
\( {\bf a}(R) \) を \(S\) まで平行移動。
\(S \to P \quad ( - d{\bf y}) \)
\( \phi_S \) を開き,\( \phi_R \) を読み込む。
\( {\bf a}(R ) \) の像を,\( {\bf a}(S) \) とする。
\( {\bf a}(S) \) を \(P\) まで平行移動。
\(P\)
\( \phi_P \) を開き,\( \phi_S \) を読み込む。
\( {\bf a}(S ) \) の像を,\( {\bf A}' \) とする。
- \( {\bf A}' - {\bf A} \) を計算する。
- この値を<一周で囲んだ面積>の値 ──即ち,\( dx \times dy \) ──で割って, 「単位面積あたり」で表す。
これを「曲率」と定義する
所謂「rotation」の手法である。
しかし,「リーマン多様体」にこの手法を使うのは,無理がある:
- 「リーマン多様体」には,「\(+dx \to +dy \to -dx \to -dy\) の長方形ループをつくれる」の含意は無い。。
- 「rotation」では,《微小ループを合併し重複をキャンセルして,任意の経路を表現》の方法で「経路に依存しない」を証明する。
しかし,「リーマン多様体」には,「このような表現が可能」の含意は無い。
「リーマン多様体」の思想は,《<空間の内にいる>のスタンスから,空間を知るための手探りをする》である。
単純設定から「曲率」の定義式を導き,そしてそれを単純な曲面図形に適用してみせることは,この「曲率」の概念に意味があるということにはならない。
この「無理」を踏まえた上で,以下,「曲率」の導出計算を見ていく。
(以下,アインシュタイン縮約表記を以て,Σ記号を省略)
各地図において,デカルト座標を \(X^i\) 座標,曲線座標を \(x^i\) 座標,と呼ぶ。
\( \phi_P \) における \( \bf A \) の \(X^i\) 座標を
\[
( a_1, \cdots, a_n )
\]
とする。
(1) \( \phi_Q \) における \( {\bf a}(Q) \) の \(x^i\) 座標
( 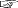 「座標の接続」
\[
\begin{align*}
a_i(Q)\ =\ a_i(P)\ +\ \Gamma^{k}_{ij}(P)\ a_k(P)\ dx^j
\end{align*}
\] 「座標の接続」
\[
\begin{align*}
a_i(Q)\ =\ a_i(P)\ +\ \Gamma^{k}_{ij}(P)\ a_k(P)\ dx^j
\end{align*}
\]
| |
ここで, \(\Gamma^{k}_{ij}\) の値が場所に依存するので,\(\Gamma^{k}_{ij}(P) \) と表した。
──以下,同様。
|
(2) \( \phi_R \) における \( {\bf a}(R) \) の \(x^i\) 座標
(
EMANの物理学 (「リーマン曲率」)
から拝借):
\[
\begin{align*}
a_i(R)\ &=\ a_i(Q)\ +\ \Gamma^{m}_{in}(Q)\ a_m(Q)\ dy^n \\
&=\ \left( a_i(P)\ +\ \Gamma^{k}_{ij}(P)\ a_k(P)\ dx^j \right) \\
& \ \ \ \ \ \ \ +\ \Gamma^{m}_{in}(Q)\ \left( a_m(P) + \Gamma^{k}_{mj}(P)\ a_k(P)\ dx^j \right) dy^n \\
& \approx \ a_i(P)\ +\ \Gamma^{k}_{ij}(P)\ a_k(P)\ dx^j \\
& \ \ \ \ +\ \left( \Gamma^{m}_{in}(P) + \frac{\partial \Gamma^{m}_{in}(P)}{\partial x^p} dx^p \right)
\left( a_m(P) + \Gamma^{k}_{mj}(P) a_k(P) dx^j \right) dy^n \\[6pt]
& (\ (P)\,を省略 \ ) \\[6pt]
&=\ a_i\ +\ \Gamma^{k}_{ij} a_k dx^j \\
& \ \ \ \ +\ \Gamma^{m}_{in} a_m dy^n\ +\ \Gamma^{m}_{in} \Gamma^{k}_{mj} a_k dx^j dy^n \\
& \ \ \ \ +\ \frac{\partial \Gamma^{m}_{in}}{\partial x^p} dx^p a_m dy^n
\ +\ \frac{\partial \Gamma^{m}_{in}}{\partial x^p} dx^p \Gamma^{k}_{mj} a_k dx^j dy^n \\
&=\ a_i \ +\ \Gamma^{k}_{ij} a_k dx^j\ +\ \Gamma^{m}_{in} a_m dy^n \\
&\ \ \ \ \ \ \ \ \ \ \ +\ \Gamma^{m}_{in} \Gamma^{k}_{mj} a_k dx^j dy^n
\ +\ \frac{\partial \Gamma^{m}_{in}}{\partial x^p} a_m dx^p dy^n \\
&\ \ \ \ \ \ \ \ \ \ \ +\ \frac{\partial \Gamma^{m}_{in}}{\partial x^p} \Gamma^{k}_{mj} a_k dx^j dy^n dx^p \\[6pt]
& (\ 最後の項は微小量3次なので,捨てる \ ) \\[6pt]
&\approx\ a_i \ +\ \Gamma^{k}_{ij} a_k dx^j\ +\ \Gamma^{m}_{in} a_m dy^n \\
&\ \ \ \ \ \ \ \ \ \ \ +\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj} a_k\ +\ \frac{\partial \Gamma^{m}_{in}}{\partial x^j} a_m \right) dx^j dy^n \\[6pt]
&=\ a_i \ +\ \Gamma^{k}_{ij} a_k dx^j\ +\ \Gamma^{m}_{in} a_m dy^n \\
&\ \ \ \ \ \ \ \ \ \ \ +\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j} \right) a_k dx^j dy^n
\end{align*}
\]
(3) \( R \rightarrow S \rightarrow P \)
この経路を, 「\( - (P \rightarrow S \rightarrow R) \)」と見る。
経路「\( P \rightarrow S \rightarrow R \)」での \(a_i(R)\) の式── \(a'_i(R)\) と表す──は,経路「\( P \rightarrow Q \rightarrow R \)」での \(a_i(R)\) の式の \( dx,\,dy \) の記号を入れ替えたものになる:
\[
\begin{align*}
a'_i(R)\ &=\ a_i \ +\ \Gamma^{k}_{ij} a_k dy^j + \Gamma^{m}_{in} a_m dx^n \\
& \ \ \ \ \ \ \ \ \ +\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j} \right) a_k dy^j dx^n
\end{align*}
\]
よって,「\( P \rightarrow Q \rightarrow R \rightarrow S \rightarrow P \)」と一周したときの座標の変化は:
\[
\begin{align*}
&a_i(R) - a'_i(R) \\[6pt]
& \ \ \ \ \ =\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j} \right) a_k dx^j dy^n \\
&\ \ \ \ \ \ \ \ \ \ -\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j} \right) a_k dy^j dx^n \\[6pt]
&\ \ \ \ \ =\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j} \right) a_k dx^j dy^n \\
&\ \ \ \ \ \ \ \ \ \ -\ \left( \Gamma^{m}_{ij} \Gamma^{k}_{mn}\ +\ \frac{\partial \Gamma^{k}_{ij}}{\partial x^n} \right) a_k dy^n dx^j \\[6pt]
&\ \ \ \ \ =\ \left( \Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j}
\ -\ \Gamma^{m}_{ij} \Gamma^{k}_{mn}\ -\ \frac{\partial \Gamma^{k}_{ij}}{\partial x^n} \right) a_k dx^j dy^n
\end{align*}
\]
ここで「\( a_k\, dx\, dy \)」を「経路が囲む面積」と見立てると,これを除した残りの
\[
\Gamma^{m}_{in} \Gamma^{k}_{mj}\ +\ \frac{\partial \Gamma^{k}_{in}}{\partial x^j}
\ -\ \Gamma^{m}_{ij} \Gamma^{k}_{mn}\ -\ \frac{\partial \Gamma^{k}_{ij}}{\partial x^n}
\]
は,「単位当たり面積」ということになる。
身分として「率」である。
この「率」を「曲率」と見なし,「点 \( x \) におけるリーマン曲率」と呼ぶ。
そして,\( R^k_{\ i,jn} \) と表す ( \(x\) は「暗黙に」ということにして,特に記号には含ませない) :
\[
\begin{align*}
R^i_{\ j,kl} \ =\ \frac{\partial \Gamma^{i}_{jl} }{\partial x^k}\ -\ \frac{\partial \Gamma^{i}_{jk}}{\partial x^l}
\ +\ \Gamma^{m}_{jl} \Gamma^{i}_{mk}\ -\ \Gamma^{m}_{jk} \Gamma^{i}_{ml}
\end{align*}
\]
|
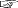 「座標の接続」
「座標の接続」