Up テンソル場 作成: 2018-01-15
更新: 2018-02-05

    「\(f\) 場」の定義図式
    の「\( E\)」を，「テンソル積 \(T = V_1 \otimes\,\cdots\,\otimes V_p \)」に換える：
    このときの「\(f\) 場」を, 「テンソル場」と謂う。


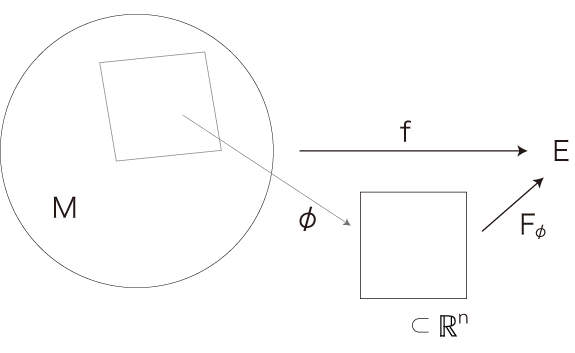
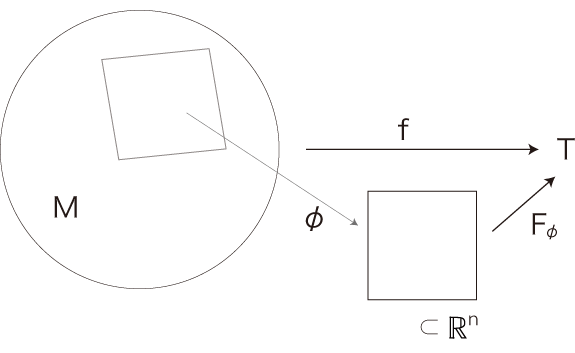
    「ベクトル場」と「テンソル場」の間に「マトリクス場」をはさんだ。
    そしてその理由を，「テンソルはマトリクスのことではないよ」を示しておくため，と述べた。

    テンソルは，マトリクスの概念の拡張ではない。
    マトリクスとは，線型写像の表現行列のことであった。
    そして \(Hom(V,W)\) は，テンソル積 \(V^* \otimes W\) と同じことになる。
    マトリクスに対応するテンソル積が \(V^* \otimes W\) だということは，テンソルがマトリクスの概念の拡張というものではないことを示す。

    ただし，物理学・工学で「テンソル」と呼ばれているもののうちには，「テンソル積」とはならないものがある。
    この場合，「加減乗除計算のワンパッケージ──計算公式」が「テンソル」と呼ばれていることになる。
    そしてこのときは，一つの計算式 \(t\) に対し，座標変換で \(t\) になる計算式全体の集合が，上の図式の中の「\(T\) に該当する。