Up 現行の「比例」主題の構成 作成: 2013-11-22
更新: 2014-05-19

    算数の「比例」は，５年で比例関係(「□が２倍，３倍，‥‥ になると，○も２倍，３倍，‥‥ 」) をやって，６年で比例定数（「ｙ＝きまった数×ｘ」）をやるようになっている．
    ただし，「ｙ＝きまった数×ｘ」は，「比例と反比例」の単元の内容になっていて，「ｘ×ｙ＝きまった数」と相対させる趣きになる．

    数学だと，構造 (空間) としての「量」をやったつぎは，これの「(準)同型」の論がきて，「比例関係」がこの「(準)同型」のことになり，さらに「比例関係の表現」(「単位を固定するときそのときの数値対応が一定数倍になるが，この定数を比例関係の単位依存の表現にする」) に進んで，これが「比例定数」の意味になる．
    「ｙ＝きまった数×ｘ」は，数学では「比例と反比例」の格好で主題になるものではない．
    ここにも数学と学校数学のずれが見られるわけである．

    ひるがえって，学校数学で比例関係と比例定数が分かたれているのは，「比例と反比例」の構成のためである．この構成がなければ，現行の「比例」教材では，比例関係と比例定数が一つの話になってしまう．
    以下，このことを示す。

    引用・参考文献にリストした23年度教科書で，比例関係と比例定数の素材および定義がどのようであるか見ていくと，つぎのようになっている：
    1. 比例関係・比例定数の素材は，つぎの形をしたものである：
      比例関係（５年)
      比例定数 (６年)
    即ち，最初に単位を定めて，数値の対応表を素材にする．
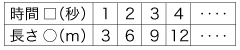
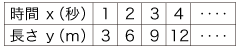
    そして，二つの表は，変数 (変項記号, variant) が違うだけで，同じものである．

    2. 比例関係・比例定数は，上の表に対してつぎのように述べられる：
      「２つの変わる量□と○があって，□が２倍，３倍，‥‥ になると，○も２倍，３倍，‥‥ になるとき，○は□に比例するといいます。」（学校図書５下, p.50）
      「２つの量ｘとｙがあって，ｙがｘに比例するとき，この関係を式で表すと，つぎのようになります。
        ｙ＝きまった数 × ｘ」（学校図書６下, p.41）
    ここでは，学校図書の教科書から文言を引いたが，各社の文言もこれと同型である．

    この記述は，文法が整合していない．不整合は，形式言語 ( 『"理論" の定式化』) ばりに□，○，ｘ，ｙが何の変項記号かを宣言すればはっきりする．それは，量ではなく数が値の変項記号になっている．

    　註 : 教育出版の教科書は，「量」ではなく「数量」のことばを用いている． また，小学校学習指導要領ないし小学校学習指導要領解説算数編では，「伴って変わる二つの数量の関係」の文言に「数量」が見える．
    この「数量」について解説しておくと，これは，「数と量」ではない。
    「個数と量」であり，「離散量と順序稠密量・完備量」( 『「数とは何か？」への答え』) である。
    すなわち，この「数量」は「量」と言っているのと同じである．


    現行は最初に単位を設定し，変項記号が数の変項記号であるようにする．
    そしてこの結果は，「□が２倍，３倍，‥‥ になると，○も２倍，３倍，‥‥ 」「ｙ＝きまった数 × ｘ」が，数値の対応表に対し横の倍を見るか縦の倍を見るかの違いになる，というものである．

      実際，５年の「比例」の授業で，「生徒が縦の倍も見てしまった」に場面展開してしまうことがあり得る．そしてこの展開を止める理屈は立たない．

    これは，「比例定数」の数学 (「比例関係の表現──単位を固定するときそのときの数値対応が一定数倍になるが，この定数を比例関係の単位依存の表現にする」) を無くしてしまうということである．


    参考・引用文献

    小学校学習指導要領 (平成20年3月改正), 第2章 各教科, 第3節 算数
    小学校学習指導要領解説 算数編 (平成20年6月改正)

    平成23年度　『小学校算数５下』『小学校算数６下』, 学校図書
    平成23年度　『小学算数５下』『小学算数６上』, 教育出版
    平成23年度　『わくわく算数５上』『わくわく算数６上』, 啓林館
    平成23年度　『たのしい算数５上』『たのしい算数６下』, 大日本図書
    平成23年度　『新しい算数５上』『新しい算数６下』, 東京書籍