夏至を考えればわかる──夏至には真東・真西で太陽が上空にあり,このとき棒の影がそれぞれ棒の真西と真東に現れる。 直線のようになるのは,秋分に理由があるということになる。 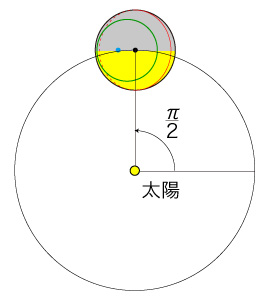
そしてもし理由づけられるとすれば,それはつぎが成り立っているということである: 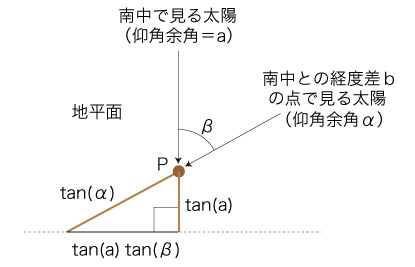
以下,推論する。 つぎのようにベクトルを定める: 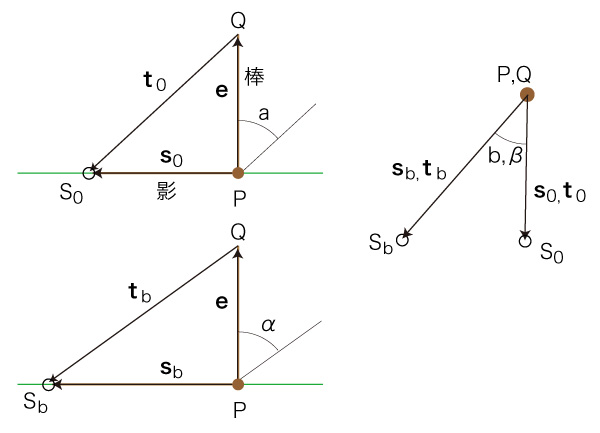
棒の長さを1とすると,つぎの長さの関係になる: 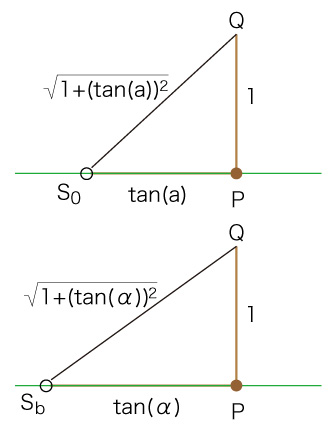
このとき \[ \begin{align} cos(b) &= \frac{ {\bf t}_b \cdot {\bf t}_0 }{ | {\bf t}_b | \ | {\bf t}_0 | } \\ \ \\ &= \frac{ ( {\bf s}_b - {\bf e} ) \cdot ( {\bf s}_0 - {\bf e} ) }{ | {\bf t}_b | \ | {\bf t}_0 | } \\ \ \\ &= \frac{ {\bf s}_b \cdot {\bf s}_0 - {\bf s}_b \cdot {\bf e}_0 - {\bf e} \cdot {\bf s}_0 + {\bf e} \cdot {\bf e} } { \sqrt{ 1 + (tan(\alpha))^2 } \ \sqrt{ 1 + (tan(a))^2 } } \\ \ \\ &= \frac{ |{\bf s}_b| |{\bf s}_0| cos(\beta ) - 0 - 0 + 1 } { \sqrt{ \frac{1}{ (cos(\alpha))^2 }} \sqrt{\frac{1}{ (cos(a))^2 }} } \\ \ \\ &= ( tan(\alpha) tan(a) cos(\beta ) + 1 ) cos(\alpha) cos(a) \\ &= sin(\alpha) sin(a) cos(\beta ) + cos(\alpha) cos(a) \\ &= sin(\alpha) sin(a) cos(\beta ) + ( cos(a) cos(b) ) cos(a) \end{align} \\ \] よって, \[ \begin{align} cos(\beta) &= \frac{ cos(b) - ( cos(a) )^2 cos(b) }{ sin(\alpha) sin(a)} = \frac{ ( sin(a) )^2 cos(b) }{ sin(\alpha) sin(a)} \\ &= \frac{ sin(a) cos(b) }{ sin(\alpha)} \end{align} \\ \] \[ \begin{align} tan(\alpha) cos(\beta) &= \frac{ sin(a) cos(b) } { cos(\alpha) } = \frac{ sin(a) cos(b)}{ cos(a) cos(b) } = \frac{ sin(a)}{ cos(a) } \\ &= tan(a) \end{align} \\ \] 所期の結果となった! |