自転する円板上での移動には，加速度がかかる。
その加速度を，ここに示す。
気象学は「進行方向を右に曲げる力 (加速度)」を教える。
しかしここで示すように，そうはならない。
移動は，右に曲げられる
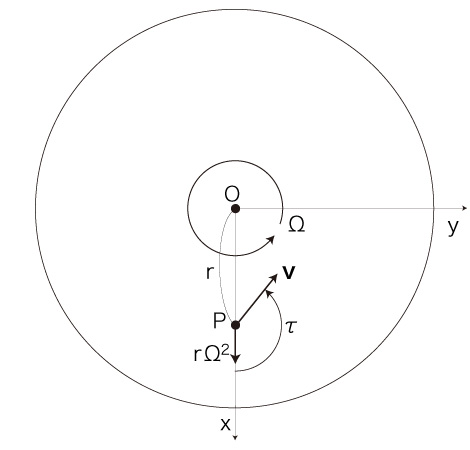加速度：
\[
\begin{align}
& \ ( - v \Omega\ sin(\tau),\ v \Omega\ cos(\tau) ) \\
& \ - ( - r \Omega^2 - v \Omega sin(\tau),\ v \Omega\ cos(\tau) ) \\
= & \ ( r \Omega^2,\ 0 )
\end{align}
\\
\]
- ＜内へ＋反回転方向へ＞移動の場合
移動は，左に曲げられる
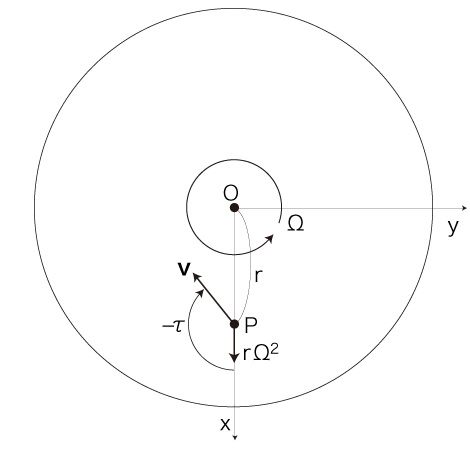加速度：
\[
\begin{align}
& \ ( v \Omega\ sin(\tau),\ v \Omega\ cos(\tau) ) \\
& \ - ( - r \Omega^2 + v \Omega sin(\tau),\ v \Omega\ cos(\tau) ) \\
= & \ ( r \Omega^2,\ 0 )
\end{align}
\\
\]
- ＜外へ＋反回転方向へ＞移動の場合
移動は，左に曲げられる
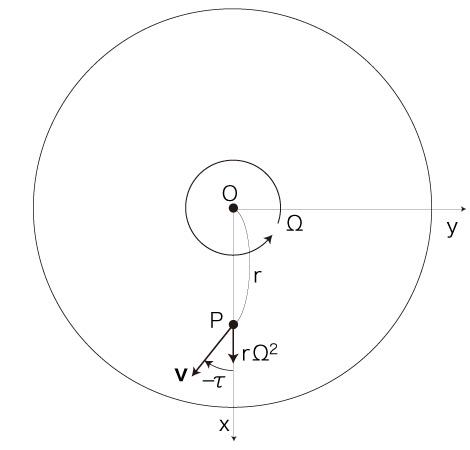加速度：
\[
\begin{align}
& \ ( v \Omega\ sin(\tau),\ - v \Omega\ cos(\tau) ) \\
& \ - ( - r \Omega^2 + v \Omega sin(\tau),\ - v \Omega\ cos(\tau) ) \\
= & \ ( r \Omega^2,\ 0 )
\end{align}
\\
\]
- ＜外へ＋回転方向へ＞移動の場合
移動は，右に曲げられる
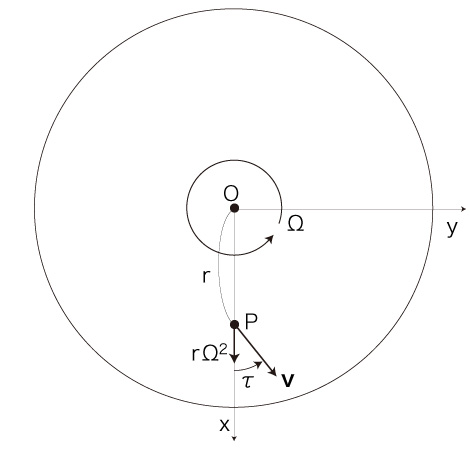加速度：
\[
\begin{align}
& \ ( - v \Omega\ sin(\tau),\ v \Omega\ cos(\tau) ) \\
& \ - ( - r \Omega^2 - v \Omega sin(\tau),\ v \Omega\ cos(\tau) ) \\
= & \ ( r \Omega^2,\ 0 )
\end{align}
\\
\]
加速度の式が引き算になっているが，これの意味は：
なお，自転球体上の移動がカオスになったように，自転円板上の移動──距離 \( r \) と速度 \( \bf{v} \) と加速度 \( r\ \Omega \) の相互フィードバック──も，カオスになりそうに思える。
これの確認も，一応予定にいれておくとする。
|
自転球体上の移動にかかる加速度