球体が,角速度 \( \Omega \) で自転しているとする。
球体の半径を \( R \) とする。
このとき, \( P \) において速度 \( \bf{v} \) の移動には,つぎの加速度がかかる:
\[
\begin{align}
( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\
& - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) ) \\
\ \\
+ ( & v\ \Omega\ cos( S_a )\ cos( P_a ) + R \Omega^2 \ cos( P_a ), \\
& v\ \Omega\ sin( P_a ) + R \Omega^2 \ cos(S_a)\ sin( P_a ), \\
& 0 ) \\
\ \\
=\ & \bigl( \
( - \frac{v^2}{R} + R \Omega^2 )\ cos( P_a ), \\
& ( - \frac{v^2}{R} + R \Omega^2 )\ cos(S_a)\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) \
\bigr) \\
\end{align}
\]
そして,
\[
\begin{align}
( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\
& - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) ) \\
\end{align}
\]
が「コリオリ力加速度」で,
\[
\begin{align}
( & v\ \Omega\ cos( S_a )\ cos( P_a ) + R \Omega^2 \ cos( P_a ), \\
& v\ \Omega\ sin( P_a ) + R \Omega^2 \ cos(S_a)\ sin( P_a ), \\
& 0 ) \\
\end{align}
\]
が「遠心力加速度」,ということになる。,
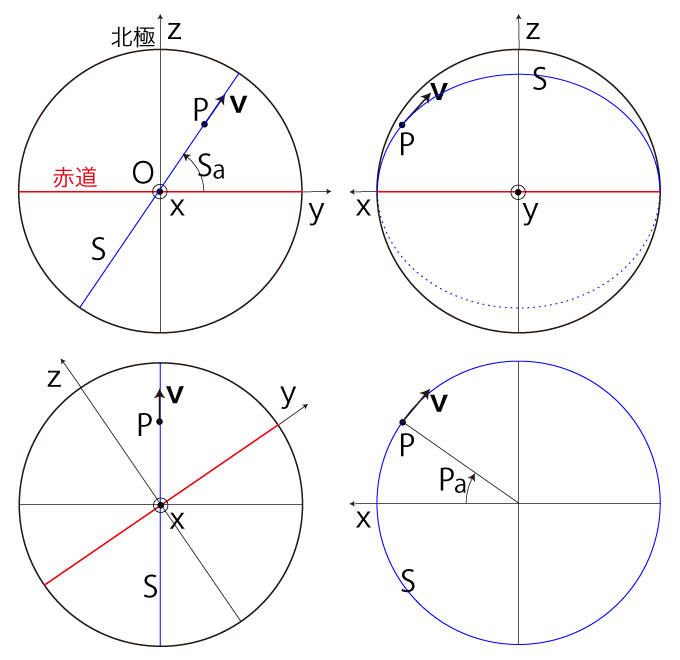
 加速度の \( (S_a,P_a) \)-表現 加速度の \( (S_a,P_a) \)-表現
ただしコリオリ力加速度は,単独では存在しない。
これは,遠心力加速度を伴う。
そして,遠心力と合わさってきっちり相殺される部分を含んでいる──上式のつぎの部分:
\[
- v\ \Omega\ cos( S_a )\ cos( P_a ) \\
- v\ \Omega\ sin( P_a )
\]
こうして移動が受ける加速度は,「コリオリ力/遠心力加速度」である。
このコリオリ力/遠心力加速度を,「地球上の移動」で計算してみよう。
\( R,\ \Omega,\ v \) を,つぎのように設定する:
\( R \) =1周4万km の球の半径の長さ
\( \Omega \) = 360度/24時間
\[
\frac{\pi}{2} R\ [m] = 10^4\ [km] = 10^7\ [m]
\ \ \Longrightarrow \ \ R = \frac{2 \times 10^7}{\pi} = 6366198\\
\ \\
\Omega\ [rad/s] \times (60 \times 60)\ [s] = \frac{\pi}{12}\ [rad] \\
\ \ \ \Longrightarrow \ \ \ \Omega = \frac{\pi}{12 \times 60 \times 60}
= \frac{\pi}{43200} = 0.000072722
\]
そして,\( v = 10,\ 100,\ 1000 m/s \) の3つの場合で,\( S_a,\ P_a \) をそれぞれ0度から90度まで,30度おきに変化させてみる。
結論から言うと,「コリオリ力/遠心力加速度」は非常に小さい。
\( v \) が非現実的な大きさにならないと,効果が見えて来ない。
気象学者は, 「コリオリ力が風の流れを曲げる」と言う。
しかしその「曲がる」は,直進の大円軌道に対して彼らが言う「曲がる」とほとんど差のつかないものである。
実際,気象学者が「コリオリ力が風の流れを曲げる」と言うとき,彼らは「直進が曲がって見える」を「コリオリ力」の意味にしているのである。──気象学者は,コリオリ力を曲解する!
|
 加速度の \( (S_a,P_a) \)-表現
加速度の \( (S_a,P_a) \)-表現