Up 加速度の \( (S_a, P_a) \)-表現 作成: 2022-06-26
更新: 2022-10-11

    ここに球体がある。
    この球体の表面を移動する。
    移動は，点 \( P \) において速度が \( {\bf{v}} \) であるとする。

    球体は，自転する球体である。
    自転は，球体の中心 \( O \) と球面上の点 \( N \) を通る直線を回転軸とし，\( O \) から \( N \) を見て右回りであるとする：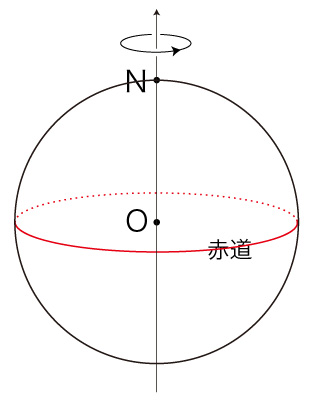

    \( P,\ \bf{v} \) に対し，\( (P, \bf{v} ) \)-座標を設定する。
    \( (P, \bf{v} ) \)-座標起点を \( Q \)， \( (P, \bf{v} ) \)-大円を \( S \) で表す。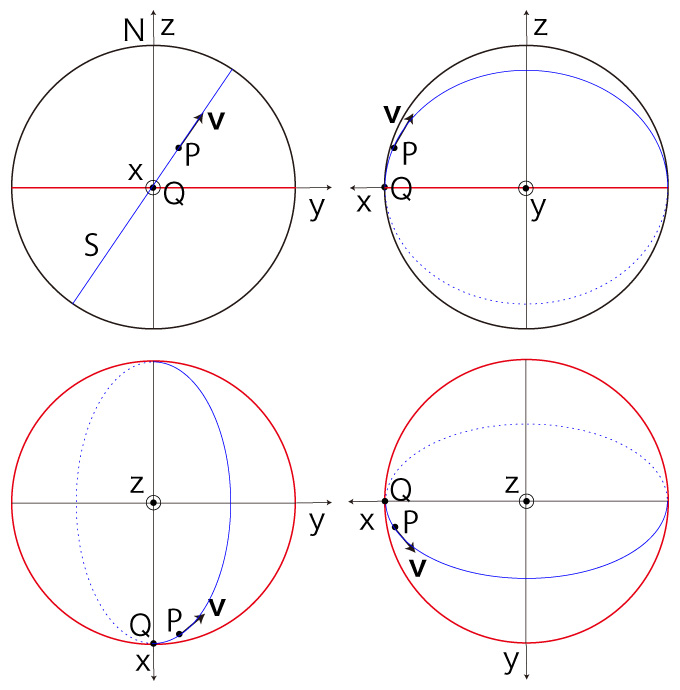

    そして，この \( (P, \bf{v} ) \)-座標を球体座標として固定する。
    この座標系からは，球体の自転が見えないことに留意せよ。
    実際，これをすることにより，＜移動＞が捉えられるようになるわけである。


    速さ \( v = | \bf{v} | \) の移動は，\( P \) での速度 \( \bf{v} \) の向きを変えることになる。
    この変化が，「加速度」に表現される。

    また移動は，位置の変化により，慣性力加速度を被ることになる。
    即ち，球体の自転による球面上の回転速度が緯度によって異なることで，緯度を変える移動は，回転速度の変化を慣性力加速度として被ることになる。

    以上を踏まえたところで，つぎの設定をする：

    時間 \( \Delta t \) で，\( P \) から点 \( P' \) に移動したとする。
    \( P' \) において移動速度が \( \bf{v'} \) になったとする。
    \( P' \) を通り \( \bf{v'} \) が接ベクトルになる大円を \( S' \) とする。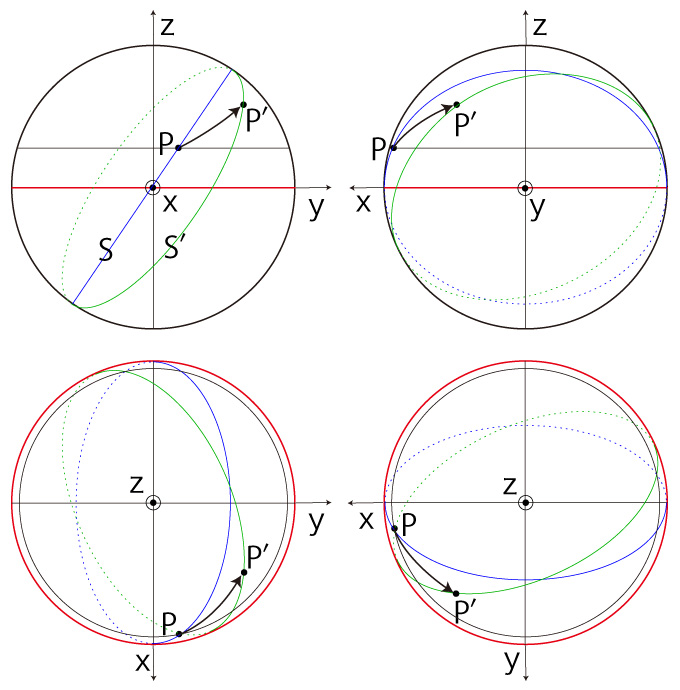


    球体の自転による \( P \) における回転速度を \( \bf{w} \)，\( P' \) における回転速度を \( \bf{w'} \) とする。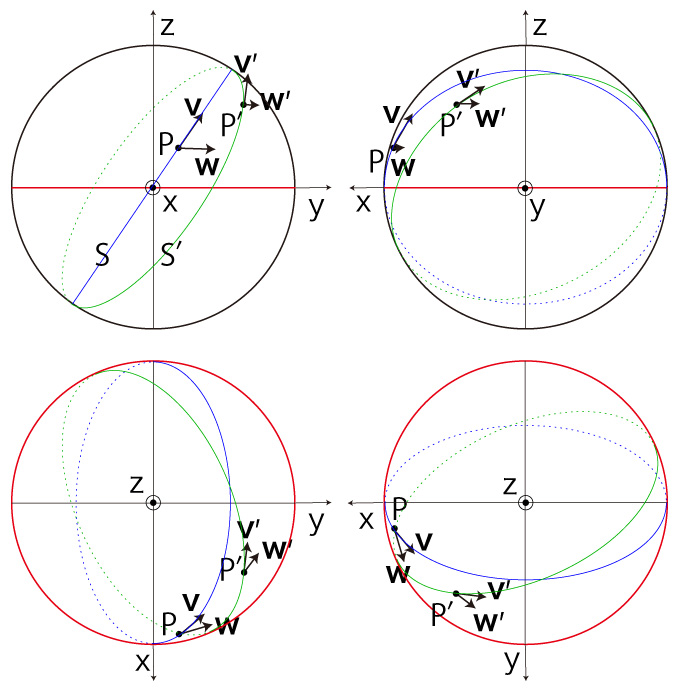

    \( ( P,\bf{v} )\)-座標は自転球体に固定の座標なので，\( P \) から \( P' \) に移動するときの速度の変化は：
      \[ ( {\bf v'} - {\bf w'} ) - ( {\bf v} - {\bf w} ) = ( {\bf v'} - {\bf v} ) - ( {\bf w'} - {\bf w} ) \]
    よって，\( P \) において移動にかかる加速度は，
        \[ \lim_{t \to 0} \frac{ {\bf v'} - {\bf v} }{ \Delta t } - \lim_{t \to 0} \frac{ {\bf w'} - {\bf w} }{ \Delta t } \ = \ \frac{ d {\bf v} }{ dt } - \frac{ d {\bf w} }{ dt } \]

    以下，この加速度を求める。


    球体の半径の長さを \( R \) とする。

    \( P = ( P_x,\ P_y,\ P_z ),\ T = ( 0,\ T_y,\ T_z ) \) を，パラメータ \( (S_a, P_a) \) で表す：
      \[ P_x = R\ cos( P_a ) \\ P_y = R\ sin( P_a )\ cos( S_a ) \\ P_z = R\ sin( P_a )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \]


    \( {\bf v} = ( v_x,\ v_y,\ v_z ) \) は， \[ v_x = - v\ sin( P_a ) \\ v_y = v\ cos( S_a )\ cos( P_a ) \\ v_z = v\ sin( S_a )\ cos( P_a ) \\ \]

    球体の自転の角速度を \( \Omega \) とする。

    \( {\bf w} = ( w_x,\ w_y,\ w_z ) \) は，
    (1) \( P \) が極のとき── \( P = ( 0,\ 0,\ \pm R ) \) のとき ──は，
      \[ {\bf w} = 0 \\ \]
    (2) \( P \) が極でないときは， \[ w_x = - R \Omega\ cos( S_a )\ sin( P_a ) \\ w_y = R \Omega\ cos( P_a ) \\ w_z = 0 \\ \]

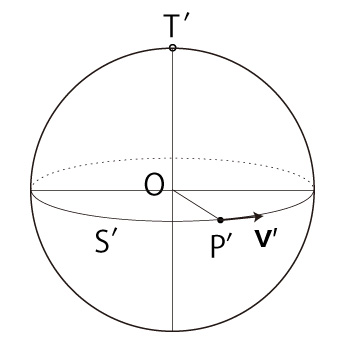
    \( \overrightarrow{OT'} \) が \( S' \) の法線ベクトルとなる点 \( T' \) をとる。

    \( T' \) の座標 \( (T'_x,\ T'_y,\ T'_z ) \) は， \[ T'_x = R\ sin( S_a ) sin(\Omega \Delta t) \\ T'_y = - R\ sin( S_a ) cos(\Omega \Delta t) \\ T'_z = R\ cos( S_a ) \]
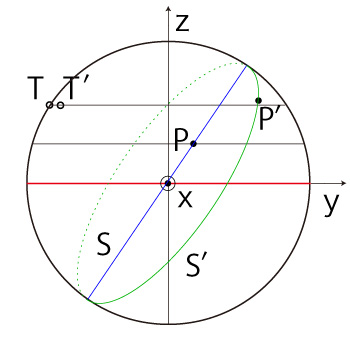      実際，\( T' \) は \( T \) をｚ軸と垂直に \( \Omega \Delta t \) 回転したところにあるので，\( OT' \) と \( ON \) のなす角の大きさは，\( S_a \) 。



    \(P' \) の座標 \( (P'_x,\ P'_y,\ P'_z ) \) は， \[ \begin{align} P'_x = R \Bigl( & cos( P_a )\ cos( (V/R) \Delta t )\ cos(\Omega \Delta t) \\ & - sin( P_a )\ sin( (V/R) \Delta t )\ cos(\Omega \Delta t) \\ & - cos(S_a)\ sin( P_a )\ cos( (V/R) \Delta t )\ sin(\Omega \Delta t) \\ & - cos(S_a)\ cos( P_a )\ sin( (V/R) \Delta t )\ sin(\Omega \Delta t) \Bigr) \\ \ \\ P'_y = R \Bigl( & cos( P_a )\ cos( (V/R) \Delta t )\ sin(\Omega \Delta t) \\ & - sin( P_a )\ sin( (V/R) \Delta t )\ sin(\Omega \Delta t) \\ & + cos(S_a)\ sin( P_a )\ cos( (V/R) \Delta t )\ cos(\Omega \Delta t) \\ & + cos(S_a)\ cos( P_a )\ sin( (V/R) \Delta t )\ cos(\Omega \Delta t) \Bigr) \\ \ \\ P'_z = R \Bigl( & sin(S_a)\ sin( P_a )\ cos( (V/R) \Delta t ) \\ & + sin(S_a)\ cos( P_a )\ sin( (V/R) \Delta t ) \Bigr) \\ \end{align} \]
      実際，つぎの関係がある：
    ]

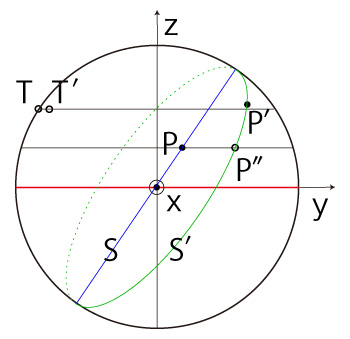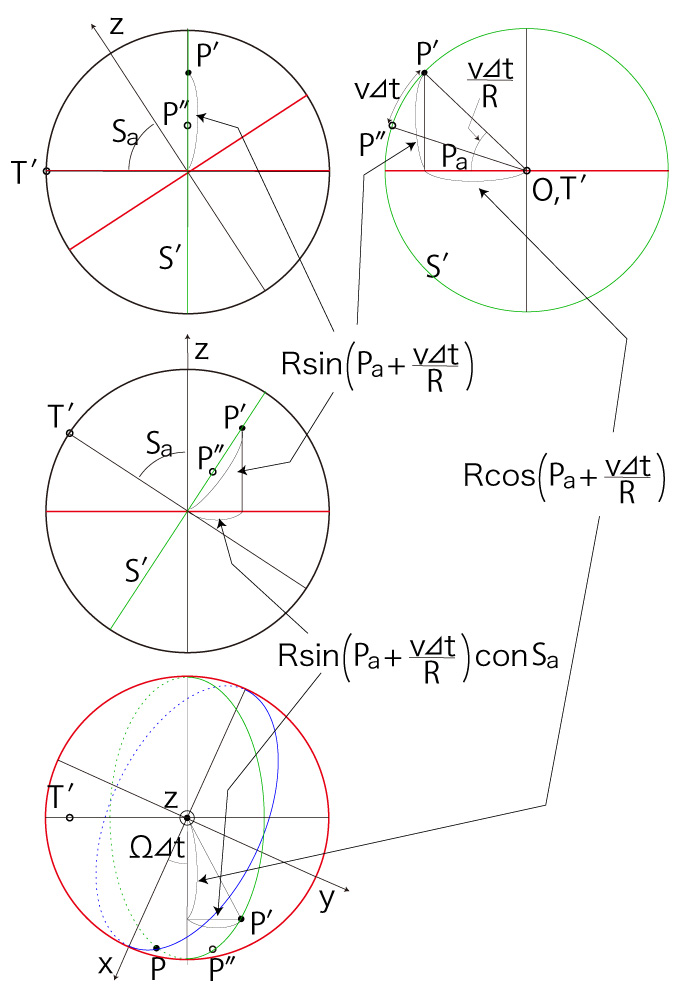
      \( R\ cos( P_a + (v/R) \Delta t ) \) と \( R\ sin( P_a + (v/R) \Delta t )\ cos(S_a) \) に，つぎの関係を適用する：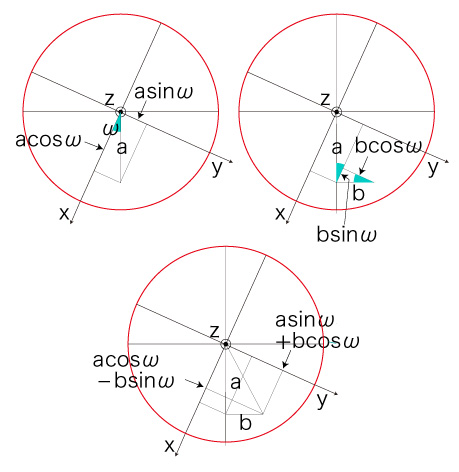


    \( {\bf v'} \) は， \[ {\bf v'} = v\ ( \\ - sin( P_a )\ cos( (v/R) \Delta t ) cos(\Omega \Delta t) \\ - cos( P_a )\ sin( (v/R) \Delta t ) cos(\Omega \Delta t)\\ - cos( S_a )\ cos( P_a )\ cos( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ + cos( S_a )\ sin( P_a )\ sin( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ , \\ \ \\ cos( S_a )\ cos( P_a )\ cos( (v/R) \Delta t )\ cos(\Omega \Delta t) \\ - cos( S_a )\ sin( P_a )\ sin( (v/R) \Delta t )\ cos(\Omega \Delta t) \\ - sin( P_a )\ cos( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ - cos( P_a )\ sin( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ , \\ \ \\ sin( S_a )\ cos( P_a )\ cos( (v/R) \Delta t ) \\ - sin( S_a )\ sin( P_a )\ sin( (v/R) \Delta t ) \\ ) \\ \]

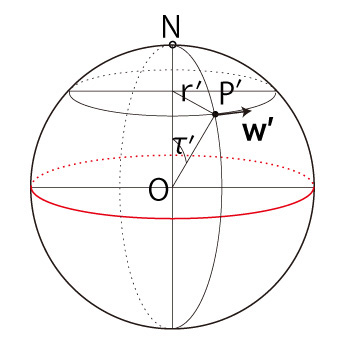
      実際， \[ {\bf v'} = |{\bf v'}|\ \frac{ \vec{OT'} \times \vec{OP'} }{ | \vec{OT'} \times \vec{OP'} |} \\ \ \\ |{\bf v'}| = v \]


    \( {\bf w'} \) は， \[ {\bf w'} = R \Omega (\\ - cos( P_a )\ cos( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ + sin( P_a )\ sin( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ - cos(S_a)\ sin( P_a )\ cos( (v/R) \Delta t )\ cos(\Omega \Delta t) \\ - cos(S_a)\ cos( P_a )\ sin( (v/R) \Delta t )\ cos(\Omega \Delta t) , \\ \ \\ cos( P_a )\ cos( (v/R) \Delta t )\ cos(\Omega \Delta t) \\ - sin( P_a )\ sin( (v/R) \Delta t )\ cos(\Omega \Delta t) \\ - cos(S_a)\ sin( P_a )\ cos( (v/R) \Delta t )\ sin(\Omega \Delta t) \\ - cos(S_a)\ cos( P_a )\ sin( (v/R) \Delta t )\ sin(\Omega \Delta t) , \\ \ \\ 0 \\ ) \]
      実際，\( \angle{ NOP' } \) の角度を \( \tau' \)，\( P' \) からｚ軸までの距離を \( r' \) とするとき， \[ {\bf w'} = | {\bf w'} |\ \frac{ \vec{ON} \times \vec{OP'} }{ | \vec{ON} \times \vec{OP'} |} \\ | {\bf w'} | = r'\ \Omega \\ r' = R\ sin( \tau' ) \\ \]



    \( {\bf v'} - {\bf v}\) は， \[ \begin{align} \longrightarrow \ \ ( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\ & - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\ & - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) \ ) \\ \ \\ & \ ( \Delta t \longrightarrow 0 ) \end{align} \]


    \( {\bf w'} - {\bf w}\) は， \[ \begin{align} \longrightarrow \ \ ( & - v\ \Omega\ cos( S_a )\ cos( P_a ) - R \Omega^2 \ cos( P_a ), \\ & - v\ \Omega\ sin( P_a ) - R \Omega^2 \ cos(S_a)\ sin( P_a ), \\ & 0 \ ) \\ \ \\ & \ ( \Delta t \longrightarrow 0 ) \end{align} \]


    結論
    球体上の移動は，速度が大円の接ベクトルになる。
    自転球体において大円 \( S \) 上で速さｖの移動は，点 \( P \) においてはつぎの加速度を受ける：
      \[ \begin{align} ( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\ & - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\ & - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) ) \\ \ \\ - ( & - v\ \Omega\ cos( S_a )\ cos( P_a ) - R \Omega^2 \ cos( P_a ), \\ & - v\ \Omega\ sin( P_a ) - R \Omega^2 \ cos(S_a)\ sin( P_a ), \\ & 0 ) \\ \ \\ =\ & \bigl( \ ( - \frac{v^2}{R} + R \Omega^2 )\ cos( P_a ), \\ & ( - \frac{v^2}{R} + R \Omega^2 )\ cos(S_a)\ sin( P_a ), \\ & - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) \ \bigr) \\ \end{align} \]