「わかりやすく」と言っても，方便の嘘をつくというのではなく，方法のエッセンスを書くということなので，ご心配無く。 温度を定義する相手は，
つぎのグラフをつくる：
対応：箱の左半分に白玉ｎ個 → これの＜場合の数＞ ただし，＜場合の数＞はとんでもなく大きくなるので，これの桁数に代える。 桁数を与える関数は，高校数学で勉強した log である：
このグラフは，つぎの形になる (  エントロピー弾性)：
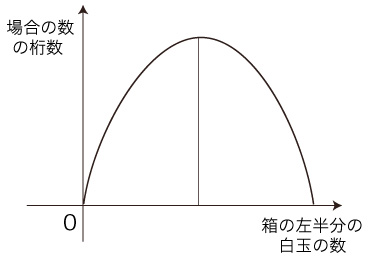
横軸の０は，「箱の左半分の白玉の数は０」。 「箱の左半分の白玉の数は０」の場合の数は，１。 そして，log(1) = 0。 グラフの頂点は：
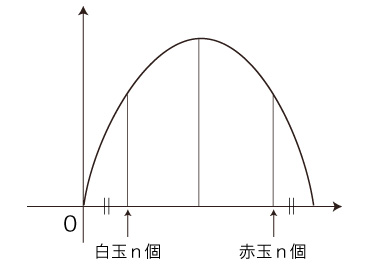 対称は重複している格好なので，グラフの右半分をカットする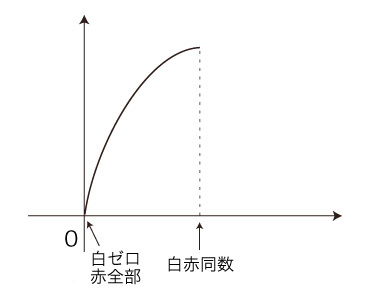：  統計力学は，このグラフの横軸，縦軸の数値を，つぎのように読む：
縦軸の数値は，「エントロピー」の数値 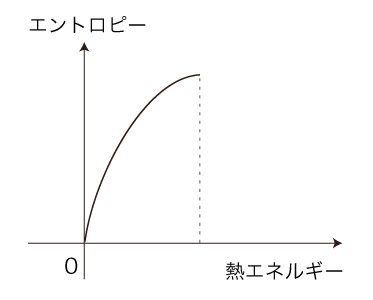 そしてここで「温度」の定義となるのだが，熱エネルギーに対するエントロピーの変化率 (グラフの接線の傾き) が「温度」と定義される。 こうして，つぎのようになる：
温度最高
温度最低 (ゼロ) 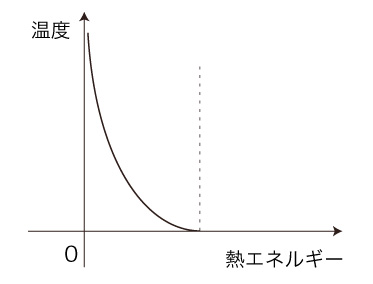 「温度」のこの定義は，つぎを意味する：
|