Up エントロピー弾性 作成: 2017-07-03
更新: 2017-07-05

    ここでは，加藤岳生『ゼロから学ぶ 統計力学』(講談社, 2013.) の pp.61-66 の内容を，つぎのように改め，書き直す：
      「全エネルギーＥ」→ 熱エネルギーＨ
      「エントロピーＳ ＝ ｋB log Ｗ」→ Ｓ ＝ log Ｗ
      「温度Ｔ」→ 温度β ＝ dＳ/dＨ


    ゴムには「熱すると短くなる」という性質がある。
    温度βで言い換えると，《ゴムは冷やすと短くなる》。

    高分子化合物を構成する分子について，つぎのように考える：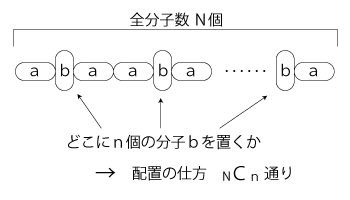
    1. 二つの構造ａ，ｂからなり，それぞれエネルギー０，εを持つ。
    2. 分子間では相互作用によるエネルギーのやりとりがあり，これにより分子がａ型になったりｂ型になったりする。
    3. ａ型分子の縦方向の長さは，ｂ型分子に比べて大きい。
      ──これは，ゴムの「熱エネルギーが増えると短くなる」「温度を冷やすと短くなる」と対応することになる。

    いま，N個の分子からなる鎖状高分子化合物があったとき，この系の温度を変化させていくと何が起こるか。

    系のいまの熱エネルギーをＨとする。
    ｂ型分子の数をｎとすると，
      ｎ ＝ Ｈ/ε

    系の状態数Ｗは，Ｎ個の分子のうちどのｎ個の分子をｂ型にするかの場合の数：
      Ｗ ＝ ＮCｎ ＝ Ｎ! / (ｎ! (Ｎーｎ)! )

    エントロピー Ｓ は，
      Ｓ ＝ log Ｗ ＝ log Ｎ! ー log ｎ! ー log (Ｎーｎ)!
    ここでスターリングの近似公式を用いて，
      Ｓ ＝ (Ｎ log Ｎ ー Ｎ) ー (ｎ log ｎ ー ｎ) ー ((Ｎーｎ) log (Ｎーｎ) ー (Ｎーｎ) )
      　 ＝ Ｎ log Ｎ ー ｎ log ｎ ー (Ｎーｎ) log (Ｎーｎ)
    さらに変形して
      　 ＝ ( (Ｎーｎ) log Ｎ ＋ ｎ log Ｎ ) ー ｎ log ｎ ー (Ｎーｎ) log (Ｎーｎ)
      　 ＝ ー ｎ log ｎ ＋ ｎ log Ｎ ー (Ｎーｎ) log (Ｎーｎ) ＋ (Ｎーｎ) log Ｎ
      　 ＝ (ーｎ) ( log ｎ ー log Ｎ ) ー (Ｎーｎ) ( log (Ｎーｎ) ー log Ｎ )
      　 ＝ ーｎ log ｎ/Ｎ ー (Ｎーｎ) log (1ーｎ/Ｎ )
      　 ＝ Ｎ ( ーｎ/Ｎ log ｎ/Ｎ ー (1ーｎ/Ｎ) log (1ーｎ/Ｎ )
      　 ＝ ーＮ ( ｐ log ｐ + (1ーｐ) log (1ーｐ ) )
    ここで，ｎ/Ｎ (全分子数に対するｂ型分子の数の割合) をｐとおいた：
      ｐ＝ｎ/Ｎ

    0 ≤ ｐ ≤ １ に留意して，Ｓ ＝ ーＮ ( ｐ log ｐ + (1ーｐ) log (1ーｐ ) ) のグラフを描く。

    つぎが ｙ＝ｘ log x ＋ (1ーｘ) log (1ーｘ) のグラフであった ( エントロピー関数)：
    そこで，つぎが Ｓ ＝ ーＮ ( ｐ log ｐ + (1ーｐ) log (1ーｐ ) ) のグラフ：
    ｎ ＝ Ｈ/ε より，
      ｐ＝ ｎ/Ｎ ＝ Ｈ/(Ｎε)
    この関係を使って，上の ｐ-Ｓグラフを Ｈ-Ｓグラフに書き直すと：

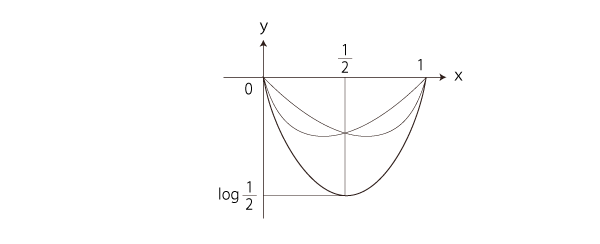
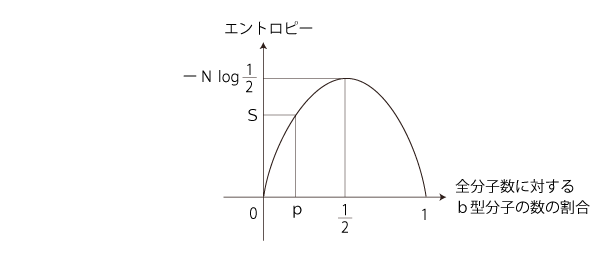
    「エントロピー増大則」を満たすのは，つぎの部分：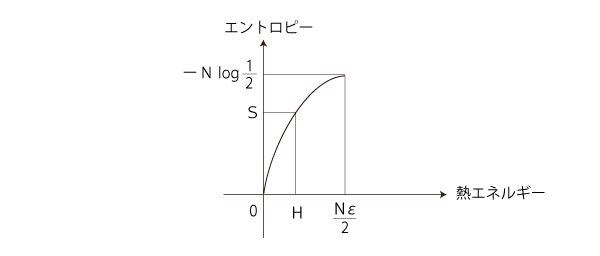

    温度β ＝ dＳ/dＨ をグラフに記入するならば：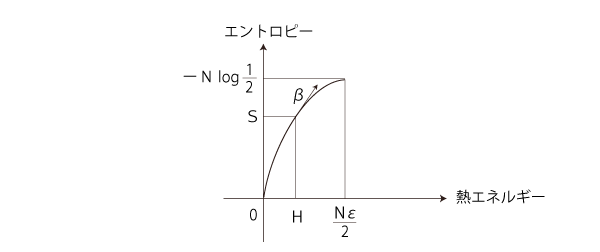


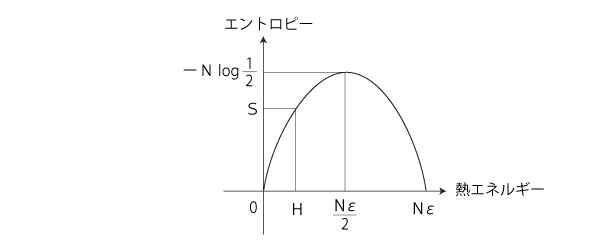
    また，このグラフから，温度βと熱エネルギーＨの対応グラフも読み取れる：
      β＝０ のとき， H ＝ Ｎε/2
      βの増加と Hの減少が対応
      β＝ ∞ と H ＝ ０ が対応

    なお，βとＨの対応式は，Ｈ ＝ Ｎε/ (ｅεβ ＋１ )
      これの計算を，以下に示す：
        β ＝ dＳ/dＨ
        　 ＝ dS/dp × dp/dＨ
        　 ＝ d(ーＮ (ｐ log ｐ + (1ーｐ) log (1ーｐ) )/dp × d(Ｈ/(Ｎε))/dＨ
        　 ＝ ーＮ ( ( log ｐ＋ p・1/p ) ＋ ( (ー1) log (1ーｐ) ＋ (1ーｐ)・(ー1/ (1ーｐ)）) × 1/(Ｎε) )
        　 ＝ ーＮ ( log ｐ＋ 1 ー log (1ーｐ) ー1 ) × 1/(Ｎε) )
        　 ＝ ー log ｐ/(1ーｐ) /ε
        よって，
        log ｐ/(1ーｐ) ＝ ーεβ
        ⇐⇒　ｐ/(1ーｐ) ＝ ｅーεβ
        ⇐⇒　ｐ ＝ (1ーｐ) ｅーεβ
        ⇐⇒　ｐ (１＋ ｅーεβ ) ＝ ｅーεβ
        ⇐⇒　ｐ ＝ ｅーεβ / (１＋ ｅーεβ ) ＝ 1 / (ｅεβ ＋１ )
        ｐ＝ Ｈ/(Ｎε) より
        Ｈ/(Ｎε) ＝ 1 / (ｅεβ ＋１ )
        ⇐⇒　Ｈ ＝ Ｎε/ (ｅεβ ＋１ )