その温度は:
赤玉が白玉と均等にばらけているときが,温度ゼロ さて,なぜこれが温度になるのか? 以下,これを説明する。 <赤玉が偏って集合している>を,「高低差がある」と読む。 <赤玉が白玉と均等にばらけている>を,「高低差がない」と読む。 統計力学は,<偏り>を表現するのに,「エントロピー」の概念をつくる:
均等にばらけているときが,エントロピー最大 高低差のある・ないから,つぎのように考えを進める:
高低差が大きいほど,この運動は大きい。」 高低差の解消は,運動が これを「運動エネルギーが無くなった」と読む。 ところで,エネルギーは「保存則」で考えている。 無くなった運動エネルギーは,どこに行ったのか? ここで,「それは熱エネルギーに変わった」と解釈する。 「エントロピー」と「熱エネルギー」のことばが出揃って,「温度」の定義で見てきたつぎのグラフになる: 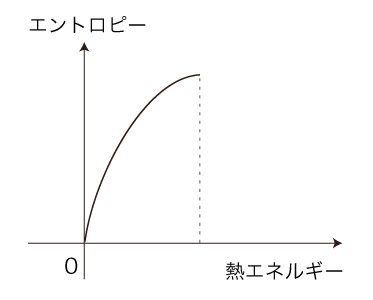 「温度」は,「熱エネルギーに対するエントロピーの変化率」と定義した。 エントロピーは
「高低差がない」は「エントロピーが大きい」 高低差を変化させているものは,運動である。 高低差の変化の大きさは,運動の大きさと対応する。 こうして,つぎのようになる:
このように,統計力学は運動の大きさを「温度」の意味にしているのである。 現前の「温度」の定義も,運動の大きさによる定義に改めていくことが探られている。 しかし運動の大きさによる「温度」の定義は,気体の温度 (「気温」) 以外では,すんなりいかないというのが実状である。──「すんなりいかない」の内容は,「この物質の "エントロピー" をどう考えたらよいかわからない」である。 |
 「温度」の定義
「温度」の定義