そして，位置移動に伴う速度変化はとんでもなく大きい (現実離れの) ものになる。 例えば Hartmann (2016), §6.4 の中のつぎの展開のように：
赤道上の物体だと，その速度は 465 m/秒。 この物体に「角運動量保存」を適用する。 そうすると，その物体は，何もせずそのまま北緯30° に移動するだけで，＜大きさが地球に相対して 134 m/秒，向きが地球の自転方向＞の速度を得る。 これは間違いである。 間違いは，事実の取り違えという初歩的な間違いである。 これである：
実際，\( u \) は，スピンの「東向き」を表現しない。 つぎは，速度ベクトル \( u,\ v,\ w \) を据えた接平面に局所デカルト座標を加え，そしてこれを垂直に真下に見た図である：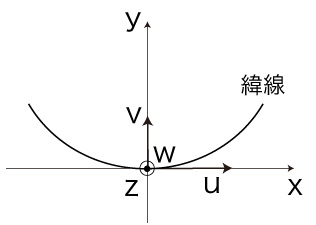 
ここで \( u \) が乗っているｘ軸は，大円Ｓに投影される。 \( u \) は，緯線を軌道とする移動の速度ではなく，Ｓを軌道とする移動の速度なのである。 そしてその移動の運動方程式は，もちろん「角運動量保存」式ではない。 初歩的な間違いであっても，これの上に込み入った装い・道具立てがいろいろ施されることによって，「科学的真理」になる。 初歩的な間違いにひとの意識が向かわないときは，だいたいが《込み入った装い・道具立てに幻惑され，騙されてしまう》なのである。 この道理，よくよく吟味すべし。
|
\[
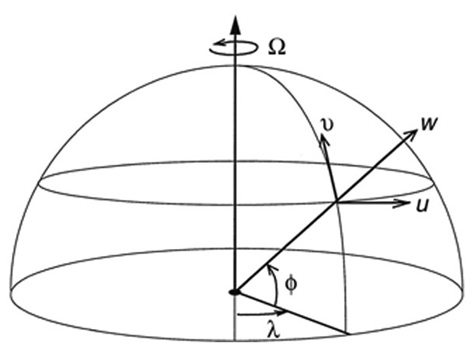u = a\ cos\phi\ \frac{ D \lambda }{ D t } = \ eastward\ wind\ speed
\]
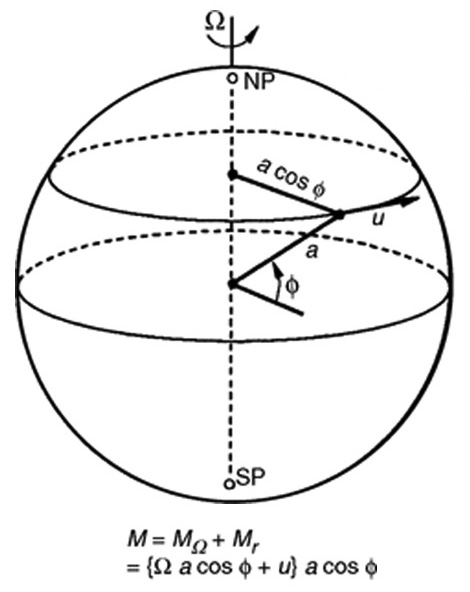
＜自転球体上の移動＞の方程式