Up 日本気象学会編『教養の気象学』から 作成: 2022-10-19
更新: 2022-10-19

      日本気象学会 (1998), pp.41,42

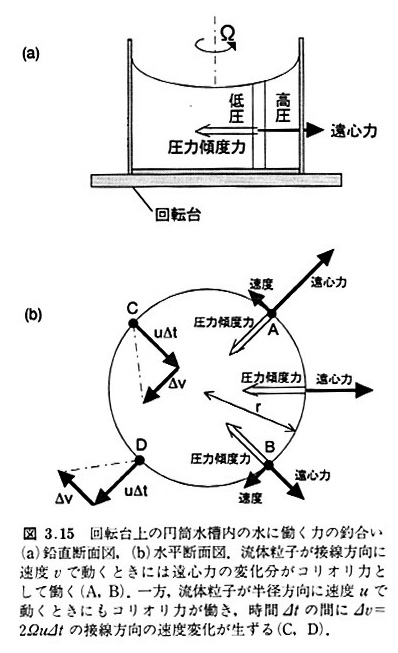
    水の入った円筒容器を回転台に載せ， 台を北半球と同じ反時計回りに回転させる.
    充分に時間がたつと， 容器内の水は回転台と一緒の回転数Ωで剛体回転するようになる.
    このとき， 水面の形は中心がくぼんだ放物面となる.
    これは， 回転する水に遠心力が働き， 内筒の縁に押しつけようとするからである.
    単位質量の流体に働く遠心力の大きさは，Vを接線方向の速度，rを回転の中心からの距離と
    するとき， V2/r で与えられる.
    水は角速度Ωで剛体回転しているので， Vは Ωｒで与えられ. 遠心力は Ω2r と書ける.
    遠心力が働くにもかかわらず，容器内に外向きの流れがないのは， 水深の違いで生ずる内向きの圧力傾度力が遠心力と釣リ合っているからである.

    　ここで， 容器内の半径ｒにある流体粒子Aを，剛体回転の速度 Ωr に比べて小さな速度ｖで回転方向 (接線方向) に動かしたときどのようなカを受けるか考えてみよう (図3.15(b)).
    粒子に働く遠心力は Ω2r から(Ωr + v)2/r へと増加する.
    この遠心力のうち， Ω2r の部分は圧力傾度力と釣り合っている
    ので， 正味で働く力は半径方向外向きに
        (Ωr + v)2/r - Ω2r = 2Ωv + v2/r
    となる.
    v は Ωr に比べて小さいので，右辺の主要な力は 2Ωv である.
    図3.15(b)で v が反対方向であれば(粒子B)， 遠心力が小さくなり， 半径方向内向さの力を受ける.
    このように. 剛体回転に相対的に接線方向に速度ｖで運動する流体粒子には， 進行方向右向きに 2Ωｖ の大きさのカが働く.

    　次に今度は半径ｒにある流体粒子Cが， 半径方向内向きに速度uで動く場合を考えよう.
    このような状態は， 例えば水槽の中心の底に穴をあけて水が
    流れ出すようにすれば実現する.
    ところで. ある点のまわりを回転する粒子に対しては. 「回転速度Vと回転中心までの距離rの積Vr は一定である」という角運動量の保存則が成り立つ.
    粒子はもともと Ωr の速度で回転しているので. 中心に移動するにつれてその回転速度は大きくなる (これと似た状況は風呂桶で栓を抜いて強い渦が発生するときにみられる>.
    回転速度が増えるのは接線方向にカを受けるためと考えられる.
    すなわち， 半径方向に運動する粒子に対して直角右・向きにカが働いたことになる.

    　このカの大きさを見積もってみよう.
    半径ｒにあった流体粒子は， 時間⊿t 後には半径 r - u⊿t に達する.
    この半径での剛体回転の速度は Ω( r - u⊿t ) である.
    これに相対的な粒子の接線速度を ⊿v とすると. 角運動量が保存するから，
        Ωr・r = { Ω( r - u⊿t ) + ⊿v} ( r - u⊿t )
    が成り立つ.
    これから，
        ( r - u⊿t ) ⊿v = 2Ωu⊿t ( r - u⊿t/2 )
    を得る.
    ⊿t が充分小さければ， 粒子の移動距離 u⊿t は最初の半径 r に比べて無視できるので
        ⊿v = 2Ωu⊿t
    となる.
    これから. 初期に剛体回転していた粒子が半径方向内向きに動き出すと接線方向に 2Ωu のカを受け. 時間⊿t の間に剛体回転に相対的な速度が 2Ωu⊿t だけ増加することがわかる.
    粒子Dが半径方向外向きに速度 uて移動する場合には，角運動量の保存から回転速度が遅くなる.
    すなわち. この場合にも粒子には進行方向に向かって直角右向きにカが働き    ， このカの大きさも 2Ωu となる.

    　以上のことから， 流体粒子が剛体回転に相対的に接線方向に動くときも，半径方向に動くときも (したがって，回転軸に直角な，どの方向に動くときも)，進行方向に向かって直角右向きに 2Ω と速度の積で与えられる力が働くことがわかる.
    このカをコリオリ(Coriolis)カとよぶ.


    この論は，騙しである。
    どこが騙しかというと，「流体粒子Cが, 半径方向内向きに速度uで動く場合を考えよう」と言いながら，「流体粒子C」を動かしてはいないからである。
    動かさないで，ワープさせる。
    その理屈は：
      「回転速度Vと回転中心までの距縫 r の積 Vr は一定」
      「回転速度が増えるのは接線方向にカを受けるためと考えられる.
      　すなわち， 半径方向に運動する粒子に対して直角右・向きにカが働いたことになる.」


    実際に「流体粒子C」を半径方向内向きに速度uで動かすとどうなるか？
    この実験は難しい。 ──念のため：上の引用文の中の「回転台」は，実験ではない。
    どうなるかは，計算で出すしかない。

    計算結果はどうなるか。
    つぎのようになる：
    特に，「進行方向に向かって直角右向きにカが働く」とはならない。


  • 引用文献
    • 日本気象学会 (1998) : 日本気象学会編『新 教養の気象学』, 朝倉書店, 1998.