気象学は「東へ」を,「緯線の上に乗る」と思う。
| |
Hartmann (2016), §6.3.1
Wind velocities in the atmosphere are measured in terms of a local Cartesian coordinate system inscribed on a sphere.
At each latitude \( \phi \) and longitude λ on a sphere of radius a, the zonal and meridional components of horizontal velocity
are defined in the following way (Fig.6.3):
 Figure 6.3
Figure 6.3
Local Cartesian coordinates on a sphere and
the zonal (u), meridional (v), and vertical (w)
components of the local vector wind velocity.
\[
\quad \quad \color{red}{ u } = a\ cos\phi\ \color{red}{ \frac{ D \lambda }{ D t } } = \color{red}{ \rm{ zonal\ or\ eastward } }\ \rm{ wind\ speed }
\]
\[
\quad \quad v = a\ \frac{ D \phi }{ D t } = \rm{ meridional\ or\ northward\ wind\ speed\ \quad \quad } (6.4)
\]
Here D/ Dt represents the material derivative – the temporal tendency that is experienced by an air parcel moving with the flow.
|
|
これは間違い。
おおもとのところで,間違っているのである:
\[
u = a\ cos\phi\ \frac{ D \lambda }{ D t } = \rm{ zonal\ or\ eastward\ wind\ speed }
\]
事実は,\( u \) は緯線の上には乗らない。
気象学は,球面幾何学の初歩的間違いをここでやっている。
つぎは,速度ベクトル \( u,\ v,\ w \) を措いた接平面:
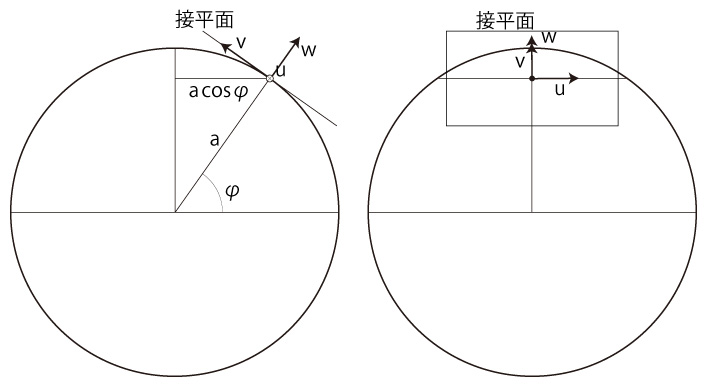

\( u \) が乗るのは,緯線ではなく,大円である。
\( u \) は,緯線を軌道とする移動の速度ではなく,大円を軌道とする移動の速度なのである。
そしてその移動の運動方程式は,当然「角運動量保存」式ではない。
「東へ」で発進した直進は,大円がこれの軌道になる:
|


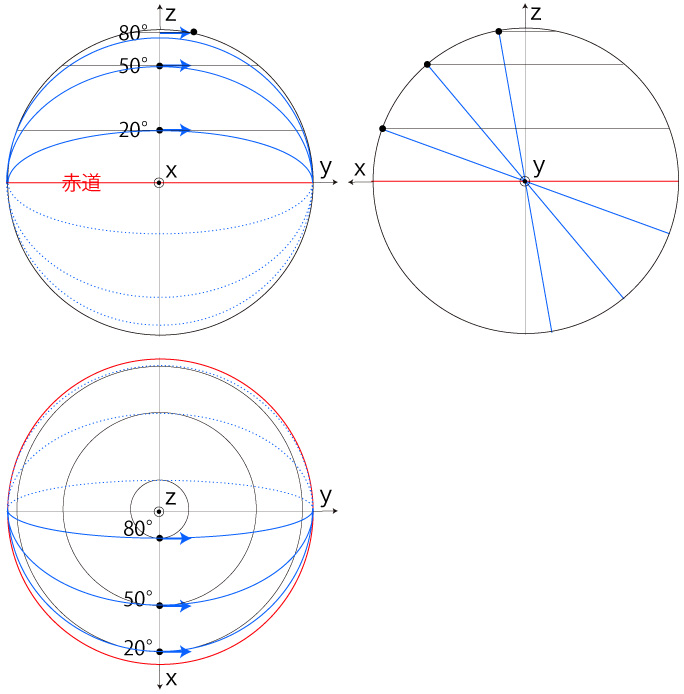

 <自転球体上の移動>の方程式
<自転球体上の移動>の方程式