ここでは,田中(2017) を引いて,気象学の唱える「コリオリ力」を改めて確認しておく。,
| |
pp.94,95
地球が自転しているときと自転していないときの人工衛星の軌道を地上に描くと,自転の効果で軌道が北半球では右方向に曲げられることを確かめることができる. ‥‥
このように,地球の回転がなければ直線的に飛行するものが,回転の影響で右に転向する効果は,おもにコリオリ力 (Coriolis force) によるものである.
ただし,正確には遠心力もはたらいているので現象の理解には注意が必要である.
北半球では,コリオリ力は物体が運動する進行方向に対して直角右向きにはたらく.
|
|
地上に描いた軌道が曲がる,という話から始まる。
で,絵の話かと思いきや,つぎには「コリオリ力は物体が運動する進行方向に対して直角右向きにはたらく」と言い出す。
気象学は,このすり替え論法をおかしいと思わない。
思わないのだから,どうしようもない。
「簡単ではない」のは,「コリオリ力」の意味を端から無視しているからである。
「コリオリ力の正しい説明」は,簡単である:
| |
p.99
‥‥ 慣性系の加速度に対して,これまでに説明した気圧傾度力や万有引力,その他の摩擦力Fがはたらいて,運動方程式が成り立っている.
\[
\frac{d_a v_a}{dt} = - \frac{1}{\rho} \nabla \rho + g^* + F
\]
これが回転系への座標変換により,回転系での加速度と関係づけられる.
\[
\frac{d_a v_a}{dt} = \frac{d_r v_r}{dt} + 2 \Omega \times v_r - \Omega^2 R
\]
したがって,回転系での加速度を左辺にして両式をまとめると以下になる.
\[
\frac{d_r v_r}{dt} = - \frac{1}{\rho} \nabla \rho - 2 \Omega \times v_r + g^*+ \Omega^2 R + F
\]
ここで,右辺はそれぞれ気圧傾度力,コリオリ力,引力,遠心力,粘性摩擦力である.
|
|
これが「コリオリ力の導出」ということになっている。
\( - 2 \Omega \times v_r \) が何故・いかなる意味で「コリオリ力」なのかという説明は無い。
これはどういうことか?
気象学は,これを「コリオリ力」の定義にしているということである。
「コリオリ力」の意味を無視する気象学には,「コリオリ力」の別物 (偽物) をつくっているという意識も無いわけである。
どうしてこんなことになったのか?
定めし,ある時どこかで何かのターニングポイントがあったのだろう。
実際,どこの学会も,珍妙な論が席巻するようになるものである。
| 註: |
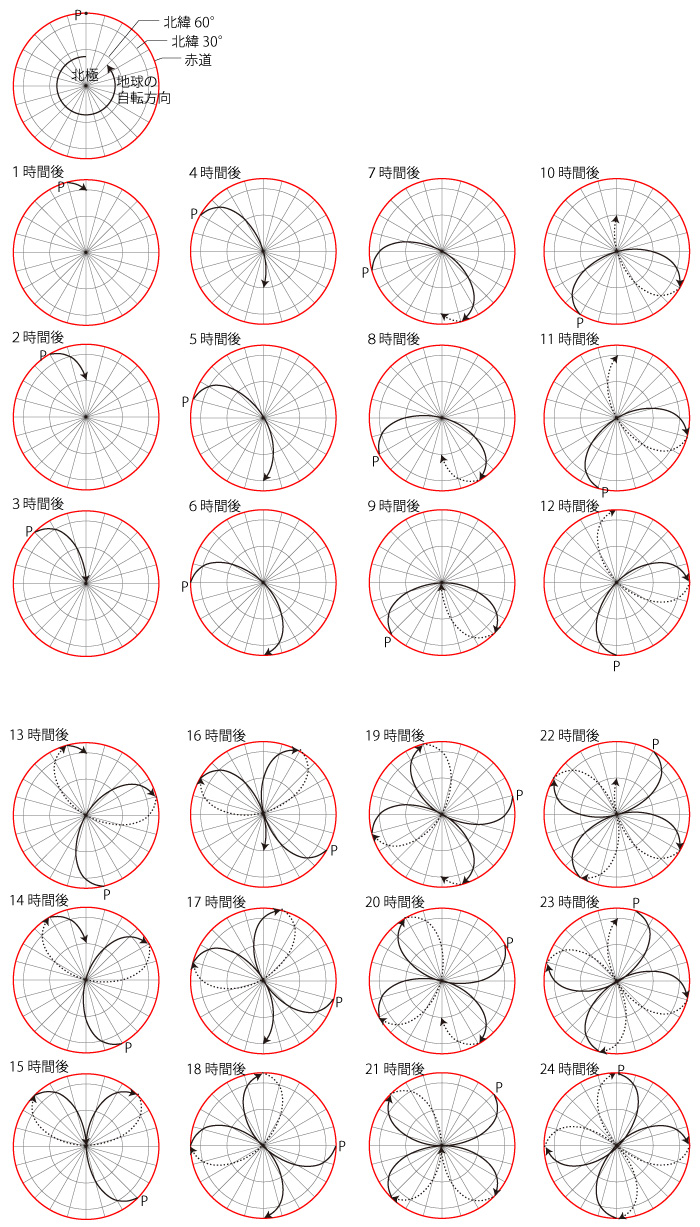
p.95 の「周期12時間で周回する極軌道衛星の軌道」の図が理解できなかったので,自分で作図してみた^^;
|
|
 「コリオリの力」とは
「コリオリの力」とは