Up \( S_a,\ P_a \) の \( (P, {\bf{v}} ) \)-座標表現 作成: 2022-06-26
更新: 2022-10-06

    \( (P, \bf{v} ) \) -座標の \( P = ( P_x,\ P_y,\ P_z ),\ T = ( 0,\ T_y,\ T_z )\) は，\( S_a,\ P_a \) によってつぎのように表された：
      \[ P_x = R\ cos( P_a ) \\ P_y = R\ sin( P_a )\ cos( S_a ) \\ P_z = R\ sin( P_a )\ sin( S_a ) \\ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \]

    ここでは，この逆をする。
    即ち，\( S_a,\ P_a \) を，\( P_x,\ P_y,\ P_z \) で表す。


    \( S \) が赤道の場合

    これは，\( P_x = R,\ P_y = P_z = 0,\ v_x = v_z = 0 \) の場合である。
    そしてこれは，\( T \) が極になっている場合，即ち \( T_y = 0,\ T_z = \pm R \) の場合である。

    このとき \( T_z \) が \( \pm R \) のいずれであるかを決めるのは，赤道に乗っている \( \bf{v} \) の方向，即ち \( v_y \)。



    このとき， \[ cos( S_a ) = cos( 0 ) = 1 \\ sin( S_a ) = sin( 0 ) = 0 \\ cos( P_a ) = cos( 0 ) = 1 \\ sin( P_a ) = sin( 0 ) = 0 \\ \]

    \( S \) が経線の場合

    これは，\( P_y = 0,\ v_y = 0 \) の場合である。
    そしてこれは，これは，\( T_y = \pm R,\ T_z = 0 \) の場合である。

    このとき \( T_y \) が \( \pm R \) のいずれであるかを決めるのは，経線に乗っている \( \bf{v} \) の方向，即ち \( v_z \)。



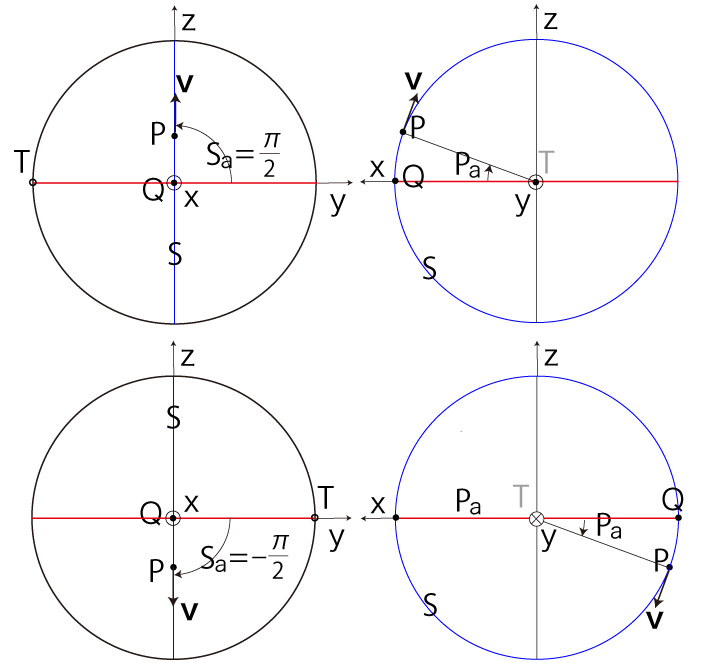
    このとき， \[ cos( S_a ) = cos \bigl( \frac{ \pi }{ 2 } \bigr) = 0 \\ sin( S_a ) = \begin{cases} sin \bigl( \frac{ \pi }{ 2 } \bigr) = 1 & ( P_z > 0 ) \\ sin \bigl( - \frac{ \pi }{ 2 } \bigr) = -1 & ( P_z < 0 ) \\ \end{cases} \\ cos( P_a ) = \frac{ P_x }{ R } \\ sin( P_a ) = \frac{ P_z }{ R } \\ \]

    \( P \) が赤道上にある場合

    これは，\( P_x = R,\ P_y = P_z = 0 \) の場合である。
    また，このとき \( T \) が定まるためには，\( v_y,\ v_z \) の両方が定まらねばならない。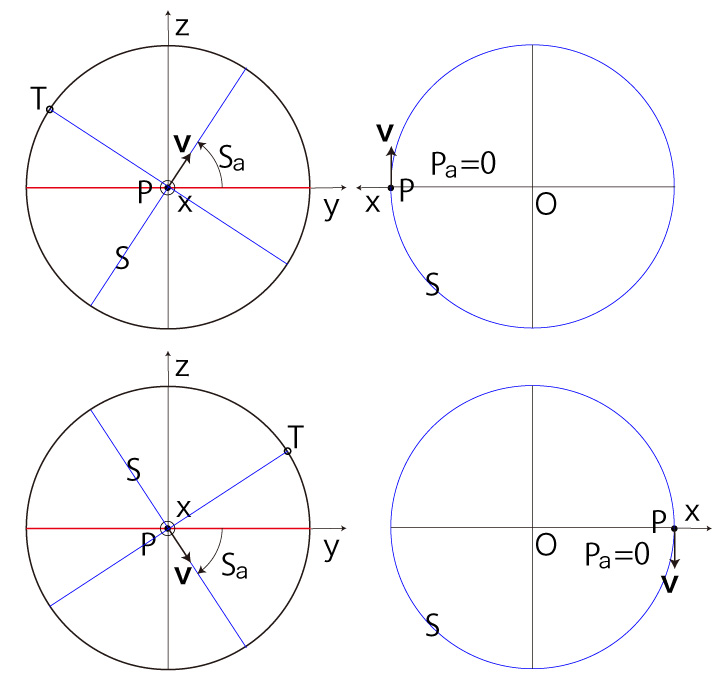



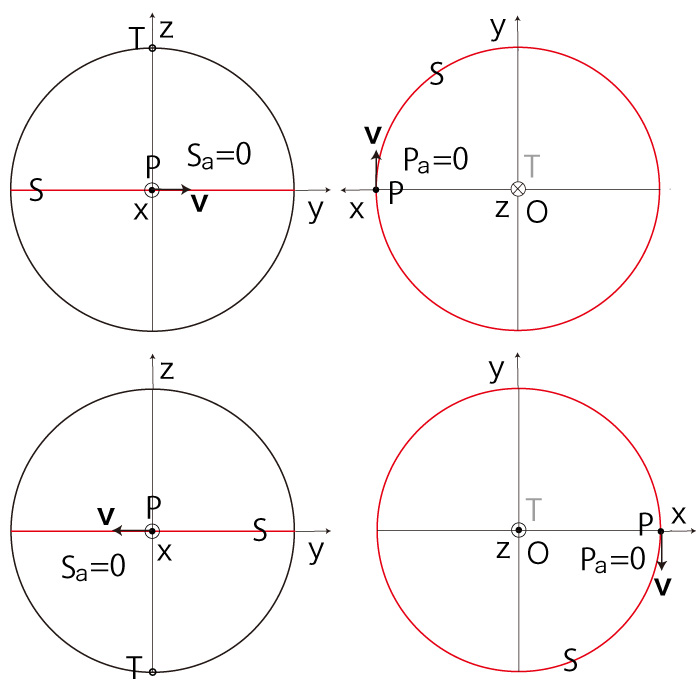
    このとき， \[ cos( S_a ) = R\ \frac{ v_y }{ v } \\ sin( S_a ) = R\ \frac{ v_z }{ v } \\ cos( P_a ) = cos( 0 ) = 1 \\ sin( P_a ) = sin( 0 ) = 0 \\ \]

    上のいずれでもない場合

    このとき， \[ T_y = - R\ \frac{ P_z }{ \sqrt{ R^2 - P_x^2 } } \\ T_z = R\ \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\ \]
    これと \[ T_y = - R\ sin( S_a ) \\ T_z = R\ cos( S_a ) \\ \] から， \[ cos( S_a ) = \frac{T_z }{R} = \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\ sin( S_a ) = - \frac{T_y }{R} = \frac{ P_z }{ \sqrt{ R^2 - P_x^2 } } \\ \] そして
      \[ P_x = R\ cos( P_a ) \\ \]
    から，
      \[ cos( P_a ) = \frac{ P_x }{ R} \\ \]
    また，
      \[ P_y = R\ sin( P_a )\ cos( S_a ) \\ \]
    からは，
      \[ P_y = R\ sin( P_a )\ cos( S_a ) \\ \quad = R\ sin( P_a )\ \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\ \]
    となり，そして \( P_y \ne 0 \) (「\( S \) は経線でない」 ) により，
      \[ 1 = \frac{ R\ sin( P_a ) }{ \sqrt{ R^2 - P_x^2 } } \\ \Longrightarrow \ sin( P_a ) = \frac{ \sqrt{ R^2 - P_x^2 } }{ R } \]


    まとめ
    (1) \( P_x = R,\ P_y = P_z = 0,\ v_x = v_z = 0 \) の場合
    　　　── \( S \) が赤道の場合
      \[ cos( S_a ) = 1 \\ sin( S_a ) = 0 \\ cos( P_a ) = 1 \\ sin( P_a ) = 0 \\ \]
    (2) \( P_y = 0,\ v_y = 0 \) の場合
    　　　── \( S \) が経線の場合
      \[ cos( S_a ) = 0 \\ sin( S_a ) = \begin{cases} 1 & ( P_z > 0 ) \\ -1 & ( P_z < 0 ) \\ \end{cases} \\ cos( P_a ) = \frac{ P_x }{ R } \\ sin( P_a ) = \frac{ P_z }{ R } \\ \]
    (3) \( P_x = R,\ P_y = P_z = 0 \) の場合
    　　　── \( P \) が赤道上にある場合
      \[ cos( S_a ) = \frac{ v_y }{ v } \\ sin( S_a ) = \frac{ v_z }{ v } \\ cos( P_a ) = 1 \\ sin( P_a ) = 0 \\ \]
    (4) 上のいずれでもない場合
      \[ cos( S_a ) = \frac{ P_y }{ \sqrt{ R^2 - P_x^2 } } \\ sin( S_a ) = \frac{ P_z }{ \sqrt{ R^2 - P_x^2 } } \\ cos( P_a ) = \frac{P_x }{R } \\ sin( P_a ) = \frac{ \sqrt{ R^2 - P_x^2 } }{ R } \\ \]