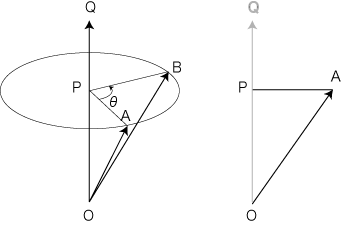
Q の座標 (qx, qy, qz)，A の座標 (ax, ay, az)，角度θ に対する B の座標 (bx, by, bz) は，直接計算して，つぎのようになりました ( 回転の計算)：
| bx ＝ |
(
cosθ
＋
qx2
ー
qx2
cosθ
)
ax
＋
(
qx
qy
ー
qx
qy
cosθ
ー
qz
sinθ
)
ay
＋
(
qx
qz
ー
qx
qz
cosθ
＋
qy
sinθ
)
az
|
| by ＝ |
(
cosθ
＋
qy2
ー
qy2
cosθ
)
ay
＋
(
qy
qz
ー
qy
qz
cosθ
ー
qx
sinθ
)
az
＋
(
qy
qx
ー
qy
qx
cosθ
＋
qz
sinθ
)
ax
|
| bz ＝ |
(
cosθ
＋
qz2
ー
qz2
cosθ
)
az
＋
(
qz
qx
ー
qz
qx
cosθ
ー
qy
sinθ
)
ax
＋
(
qz
qy
ー
qz
qy
cosθ
＋
qx
sinθ
)
ay
|
これを，つぎのように変形します：
bx ＝
(
cosθ
＋
qx2
ー
qx2
cosθ
)
ax
＋
(
qx
qy
ー
qx
qy
cosθ
ー
qz
sinθ
)
ay
＋
(
qx
qz
ー
qx
qz
cosθ
＋
qy
sinθ
)
az
＝
(
cos2(θ/2)
ー
sin2(θ/2)
＋
qx2
ー
qx2
( 1 ー 2 sin2(θ/2) )
)
ax
＋
(
qx
qy
ー
qx
qy
( 1 ー 2 sin2(θ/2) )
ー
qz
2 cos(θ/2) sin(θ/2)
)
ay
＋
(
qx
qz
ー
qx
qz
( 1 ー 2 sin2(θ/2) )
＋
qy
2 cos(θ/2) sin(θ/2)
)
az
＝
(
cos2(θ/2)
ー
(
qx2
＋
qy2
＋
qz2
)
sin2(θ/2)
＋ 2
qx2
sin2(θ/2)
)
ax
＋ 2
(
ー
cos(θ/2)
qz
sin(θ/2)
＋
qx
sin(θ/2)
qy
sin(θ/2)
)
ay
＋ 2
(
cos(θ/2)
qy
sin(θ/2)
＋
qx
sin(θ/2)
qz
sin(θ/2)
)
az
＝
(
cos2(θ/2)
＋
qx2
sin2(θ/2)
ー
qy2
sin2(θ/2)
ー
qz2
sin2(θ/2)
)
ax
＋ 2
(
ー
cos(θ/2)
qz
sin(θ/2)
＋
qx
sin(θ/2)
qy
sin(θ/2)
)
ay
＋ 2
(
cos(θ/2)
qy
sin(θ/2)
＋
qx
sin(θ/2)
qz
sin(θ/2)
)
az
同様に：
| by ＝ |
(
cos2(θ/2)
ー
qx2
sin2(θ/2)
＋
qy2
sin2(θ/2)
ー
qz2
sin2(θ/2)
＋ 2
(
ー
cos(θ/2)
qx
sin(θ/2)
＋
qy
sin(θ/2)
qz
sin(θ/2)
)
az
＋ 2
(
cos(θ/2)
qz
sin(θ/2)
＋
qx
sin(θ/2)
qy
sin(θ/2)
)
ax
|
| bz ＝ |
(
cos2(θ/2)
ー
qx2
sin2(θ/2)
ー
qy2
sin2(θ/2)
＋
qz2
sin2(θ/2)
)
az
＋ 2
(
ー
cos(θ/2)
qy
sin(θ/2)
＋
qx
sin(θ/2)
qz
sin(θ/2)
)
ax
＋ 2
(
cos(θ/2)
qx
sin(θ/2)
＋
qy
sin(θ/2)
qz
sin(θ/2)
)
ay
|
そしてこれを，つぎの「３次元実ベクトルで閉じる四元数倍のパターン」( ３次元ベクトルの四元数倍は？) と比較します：
| |
(fr ＋ fx i ＋ fy j ＋ fz k )
×
(ax i ＋ ay j ＋ az k )
×
(fr ー fx i ー fy j ー fz k )
＝ (
(
fr2
＋
fx2
ー
fy2
ー
fz2
)
ax
＋ 2 (
ー
fr
fz
＋
fx
fy
)
ay
＋ 2 (
fr
fy
＋ 2
fx
fz
)
az
) i
＋ (
(
fr2
ー
fx2
＋
fy2
ー
fz2
)
ay
＋ 2 (
ー
fr
fx
＋
fy
fz
)
az
＋ 2 (
fr
fz
＋
fx
fy
)
ax
) j
＋ (
(
fr2
ー
fx2
ー
fy2
＋
fz2
)
az
＋ 2 (
ー
fr
fy
＋
fx
fz
)
ax
＋ 2 (
fr
fx
＋
fy
fz
)
ay
) k
|
この比較から，つぎの公式を得ます：
(
cos(θ/2)
＋ qx sin(θ/2) i
＋ qy sin(θ/2) j
＋ qz sin(θ/2) k
)
×
(ax i
＋ ay j
＋ az k)
×
(
cos(ーθ/2)
＋ qx sin(ーθ/2) i
＋ qy sin(ーθ/2) j
＋ qz sin(ーθ/2) k
)
＝
bx i
＋by j
＋bz k
|
