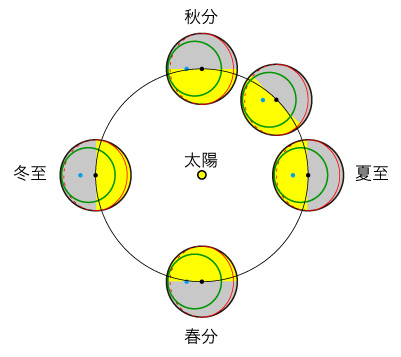
計算モデルとして,つぎの条件を立てる: 「緯度 a」は,つぎの図に示される角度aである: 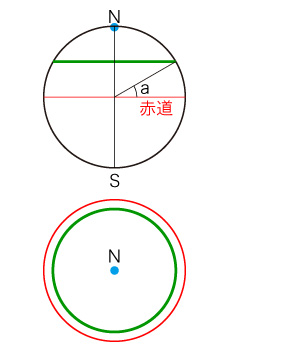
公転平面に対する地軸の傾きを,nとする: 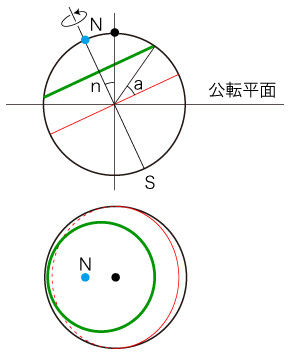
公転角度を,夏至が0であるように定義する: 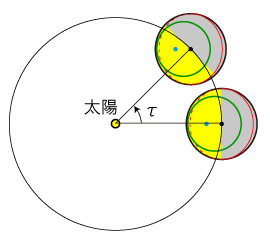 sin, cos を適用する角度の数値は,ラジアンを単位とした数値である。 ラジアンの意味を確認すべし: 「公転角速度一定」の条件について: この条件には,つぎの含蓄がある:
公転軌道の形──公転軌道が楕円であるとか──は,これに関係しない。 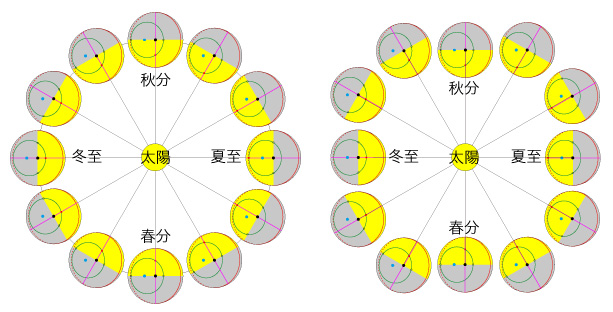
|
| Up | 公理 (計算モデル) | 作成: 2020-09-03 更新: 2020-10-04 |

計算モデルとして,つぎの条件を立てる: 「緯度 a」は,つぎの図に示される角度aである: 
公転平面に対する地軸の傾きを,nとする: 
公転角度を,夏至が0であるように定義する:  sin, cos を適用する角度の数値は,ラジアンを単位とした数値である。 ラジアンの意味を確認すべし: 「公転角速度一定」の条件について: この条件には,つぎの含蓄がある:
公転軌道の形──公転軌道が楕円であるとか──は,これに関係しない。 
|