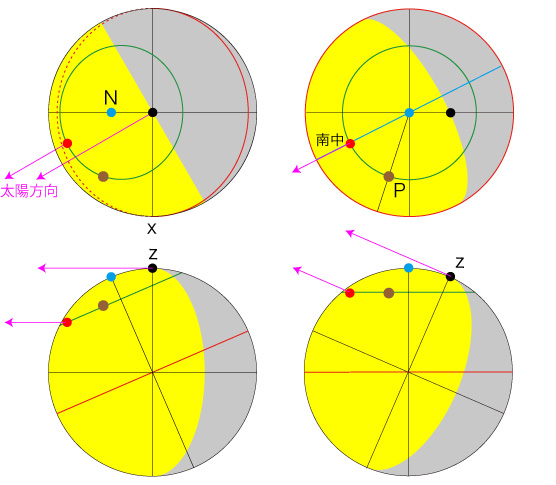
Ｐには，地平面に垂直に棒を立てられている。 棒の長さの数値を１とする。 緯度ｓでの太陽の仰角余角を \( \alpha_s \) とし，経度ｂでの仰角余角を \( \alpha_b \) とする。 経度ｓでは地平面上に長さ \( tan( \alpha_s ) \) の影ができ，経度ｂでは長さ \( tan( \alpha_b )\) の影ができる。 その影を，それぞれ地面に刻んで記録する。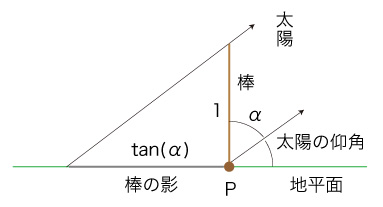 
ここで，南中点の経度ｓは，\(n, \tau, a\) によって，つぎのように表される。 (  南中点の経度計算式)：
\[
cos( s ) = \frac { \tau_s} {\sqrt{ 1 - (n_s)^2 ( \tau_c )^2 } }
\]
そして \( \alpha_s \) が，つぎのように表される。 ( 南中太陽の高度)：
\[
cos( \alpha_s ) = a_c \sqrt{ 1 - (n_s)^2 ( \tau_c )^2 } + n_s a_s \tau_c \\
\\ \\ \\
\]
\( \alpha_b \) は，つぎのように表される。
( 緯度ａ経度ｂで見る太陽の高度)：
\[
cos( \alpha_b ) = a_c \tau_s \ b_c - n_c a_c \tau_c \ b_s + n_s a_s \tau_c
\\ \ \\
\]
Ｐが南中点にあったときの影といまの影のなす角度をβとする。
βは，\( n, \tau, a, b \) で表されるはずである。 この式を求める。 ｂとｓの差をｐとすると，ｐとβがつぎの関係になる：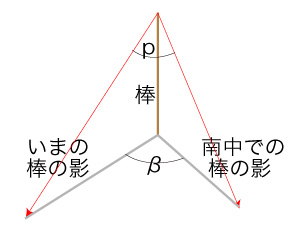 
ベクトルをつぎのように定める：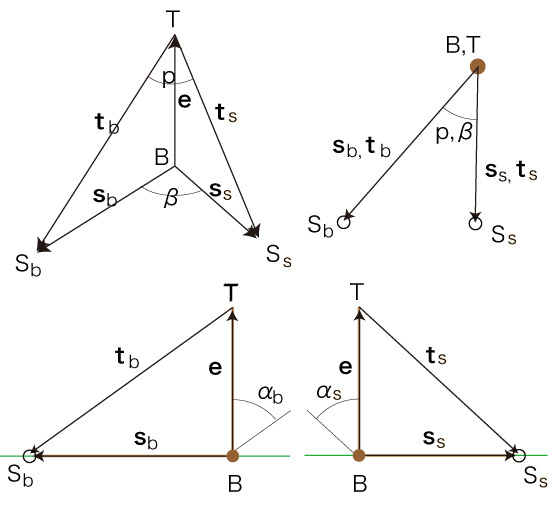 
つぎの長さの関係がある：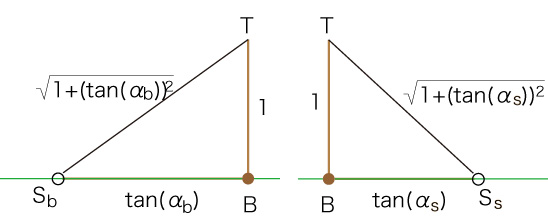 
よって， \[ \begin{align} cos(p) &= \frac{ {\bf t}_b \cdot {\bf t}_s }{ | {\bf t}_b | \ | {\bf t}_s | } \\ \ \\ &= \frac{ ( {\bf s}_b - {\bf e} ) \cdot ( {\bf s}_s - {\bf e} ) }{ | {\bf t}_b | \ | {\bf t}_s | } \\ \ \\ &= \frac{ {\bf s}_b \cdot {\bf s}_s - {\bf s}_b \cdot {\bf e} - {\bf e} \cdot {\bf s}_s + {\bf e} \cdot {\bf e} } { \sqrt{ 1 + (tan(\alpha))^2 } \ \sqrt{ 1 + (tan(\alpha_s))^2 } } \\ \ \\ &= \frac{ |{\bf s}_b| |{\bf s}_s| cos(\beta ) - 0 - 0 + 1 } { \sqrt{ \frac{1}{ (cos(\alpha))^2 }} \sqrt{\frac{1}{ (cos(\alpha_s))^2 }} } \\ \ \\ &= ( tan(\alpha) tan(\alpha_s) cos(\beta ) + 1 ) cos(\alpha) cos(\alpha_s) \\ &= sin(\alpha) sin(\alpha_s) cos(\beta ) + cos(\alpha) cos(\alpha_s) \end{align} \\ \ \\ \Longrightarrow \ \ cos(\beta ) = \frac{ cos(p) - cos(\alpha) cos(\alpha_s) }{ sin(\alpha) sin(\alpha_s) } \\ \ \\ \] ここまでのまとめ \[ cos(\beta ) = \frac{ cos(b - s) - cos(\alpha_b) cos(\alpha_s) }{ sin(\alpha_b) sin(\alpha_s) } \\ \ \\ cos( s ) = \frac { \tau_s} {\sqrt{ 1 - (n_s)^2 ( \tau_c )^2 } } \\ \ \\ cos( \alpha_s ) = a_c \sqrt{ 1 - (n_s)^2 ( \tau_c )^2 } + n_s a_s \tau_c \\ \ \\ cos( \alpha_b ) = a_c \tau_s \ b_c - n_c a_c \tau_c \ b_s + n_s a_s \tau_c \\ \ \\ \] ｋ時の経度を \( b_k \)，影と南中の影のなす角を \( \beta_k \)，そして太陽の仰角余角を \( \alpha_k \) とする。 このとき， \[ cos(\beta_k ) = \frac{ cos(b_k - s) - cos(\alpha_k) cos(\alpha_s) }{ sin(\alpha_k) sin(\alpha_s) } \\ \ \\ cos( \alpha_k ) = a_c \tau_s \ (b_k)_c - n_c a_c \tau_c \ (b_k)_s + n_s a_s \tau_c \\ \ \\ \] 正午の経度を Mb とすると， \[ Mb = \frac{3}{2} \pi + \tau \\ b_k = Mb + ( 15 \times ( k - 12 ) ) \] まとめ
|