このとき「エントロピー弾性」の H-Sグラフは,つぎが「系の状態で最も確率の高いものの実現」の内容であることを示している:  エントロピー弾性 エントロピー弾性
ここで,「b型が全体の半分」に着目する。 実は,「エントロピー弾性」の論では,「熱エネルギー」の語が空回りしている。 論の中で「熱エネルギー」として機能しているものは,専ら「b型が全体に占める割合」である。 このことは,つぎのように言ってかまわないことを示している:
赤玉,白玉が同数入った箱をずっと振っていくと,均質に混ざったところで落ち着く。 これは,よく「エントロピー」の主題にされる。 しかしその論者は,この場合の<熱エネルギー → エントロピー>関数を示さない。 ここで,この関数をここで定めるとしよう。 「熱エネルギー」概念の形式性を確認することが,ここでの目的である。 やることは,上の「エントロピー弾性」の方法「b型が全体に占める割合」をなぞることである。 <熱エネルギー → エントロピー>関数はつぎのように定めればよい: この<熱エネルギー → エントロピー>関数を,実際に求めてみよう。 n個の赤玉が左側にある組み合わせの数Wは,N! × N! /((Nーn)! × (Nーn)! × n! × n!)
赤玉N個からn個をとる組み合わせの数は,NCn。 白玉N個から Nーn個をとる組み合わせの数は,NCn。 よって,n個の赤玉が左側にある組み合わせの数Wは:
= N! /((Nーn)! × n!) × N! /((Nー(Nーn)! × (Nーn!) = N! × N! /((Nーn)! × (Nーn)! × n! × n!) S = ーM ( H log H + (1ーH) log(1ーH ) ) ──ここで,M=2N (玉の総数)。
= log (N! × N! /((Nーn)! × (Nーn)! × n! × n!)) = 2 log N! ー2 log(Nーn)! ー 2 log n! スターリングの近似公式を適用して = 2 (N logNー N) ー2 ((Nーn) log(Nーn) ー (Nーn)) ー 2(nlog nーn) = 2 (N logNー N ー (Nーn) log(Nーn) + (Nーn) ー nlog n+n) = 2 (N logN ー (Nーn) log(Nーn) ー nlog n ) = 2 ( ーn( log nー log N ) ー (Nーn) ( log(Nーn) ー log N ) = ー2N ( n/N log n/N + (1ーn/N) log (1ーn/N) ) = ーM ( H log H + (1ーH) log(1ーH ) ) y = x log x + (1ーx) log(1ーx ) のグラフは,既に求めている: 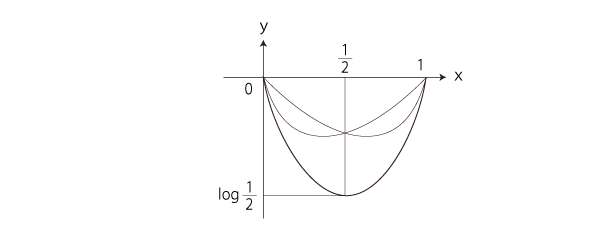
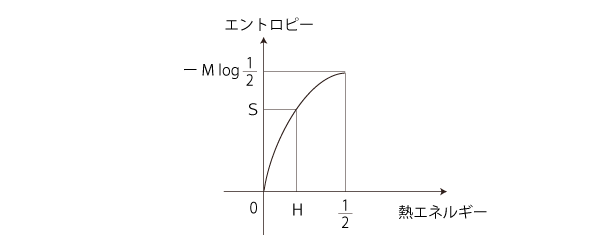
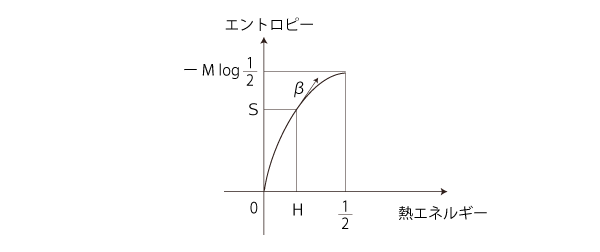
このグラフから,温度βと熱エネルギーHの対応グラフも読み取れる:
βの増大と Hの減少が対応 β= ∞ と H = 0 が対応 実際,関数:β├→ H の式は,H = 1 / (eεβ +1 ) ── ここで,ε = 1/M。
= d(ーM (H log H + (1ーH) log (1ーH) )/dH = ーM ( ( log H+ H・1/H ) + ( (ー1) log (1ーH) + (1ーH)・(ー1/ (1ーH))) = ーM ( log H+ 1 ー log (1ーH) ー1 ) = ーM log H/(1ーH) ⇐⇒ H/(1ーH) = eーεβ ⇐⇒ H = (1ーH) eーεβ ⇐⇒ H (1+ eーεβ ) = eーεβ ⇐⇒ H = eーεβ / (1+ eーεβ ) = 1 / (eεβ +1 ) |