| |
田中(2007), p.43
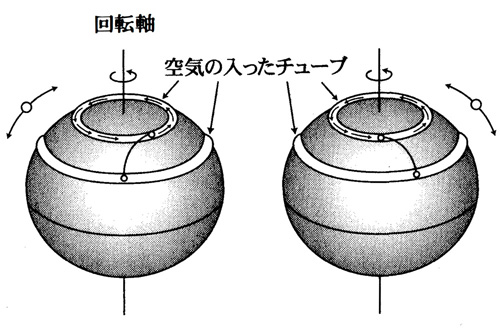
はじめに、地面に対して静止した (つまり地球の自転とともに回転する) チューブが東西に地球を一回りしているとする。
もし、このチューブが中緯度から高緯度に移動したとすると、あとで述べる角運動量の保存則により回転半径の縮まったチューブは東向きに回りだす。
チューブの中の空気塊は、北に移動することで東向きの加速度を受けるが、これがコリオリ力である。
地面に対して東向きに回りだしたチューブには、今度は遠心力の増大により回転半径の大きい低緯度に広がろうとする力が働く。
東向きに移動する空気塊は南向きの加速度を受けるが、これもコリオリ力である。
はじめの緯度を通過して低緯度に向かうチューブは、角運動量の保存により今度は西向きに回りだす。
西に移動するチューブは遠心力が低下するので、高緯度に向かい、はじめの位置に戻る。
このように、回転する地球上のチューブは回転を速めたり逆向きに回転したりしながら、南北に振動する。
チューブの中の間じ質量を持つ空気塊の動きを追ってみると、それは円運動を描くことが確かめられる。
コリオリ力とは、回転する地球上で、水平運動という束縛を受けたときに、回転の角運動量を保存するように運動方向と直角に働く力である。
|
|
気象学にとって，自転体上の流体粒子は，「充分に訓練された結果，剛体回転するようになった物体」である (  気象学者の＜流体粒子＞物性観 )
そして気象学は，この剛体回転に「角運動量保存」が適用できると思う。
しかし気象学は，ここでさらに，初歩的間違いを重ねる。
「角運動量保存」が適用される現象を，取り違えるのである。
「角運動量保存」が適用される現象は，自転体が形を変えるとか回転軸に垂直に移動するとかではない。
適用される現象は，独楽が傾きながら大きく回る運動である。
自転チューブだと，つぎの現象ということになるのである：
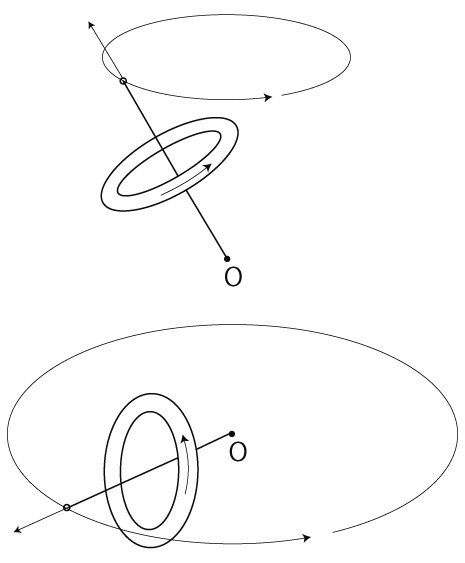註. 角運動量の方向は, 「自転体の回転方向で右ネジが進む方向」で定義される。
気象学が「角運動量保存」を説くなかには，フィギュアスケートのスピンの「伸ばした腕を縮めると回転速度が増す」を「角運動量保存」の例にしたりするものもある。
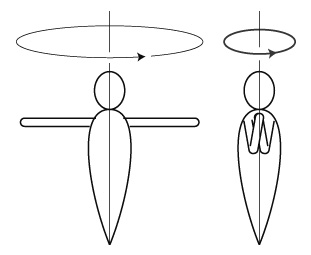
間違いである。
これの説明になるのは，「角運動量保存」ではない。
「体の一部の回転速度が減る分に応じて，体全体の回転が’加速される」という話である。
実際，フィギュアスケートのスピンを「角運動量保存」の話にするときは，つぎの絵を描くことになる：
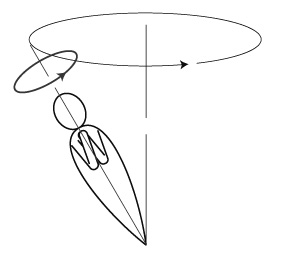
- 引用文献
- 田中博 (2007) :『偏西風の気象学』(気象ブックス016)), 成山堂, 2007.
|
