つぎは,自転球体上の移動軌跡をシミュレートしたものである :
シミュレーション1
赤道で北へ発したときの,その後の移動軌跡
(完全に北向きだと直進になるので,発進の向きをわずかに東に傾けた)
 北緯20°, 50°, 80° のそれぞれで「東へ」初速 50 m/s で発したときの,その後の移動軌跡
北緯20°, 50°, 80° のそれぞれで「東へ」初速 50 m/s で発したときの,その後の移動軌跡
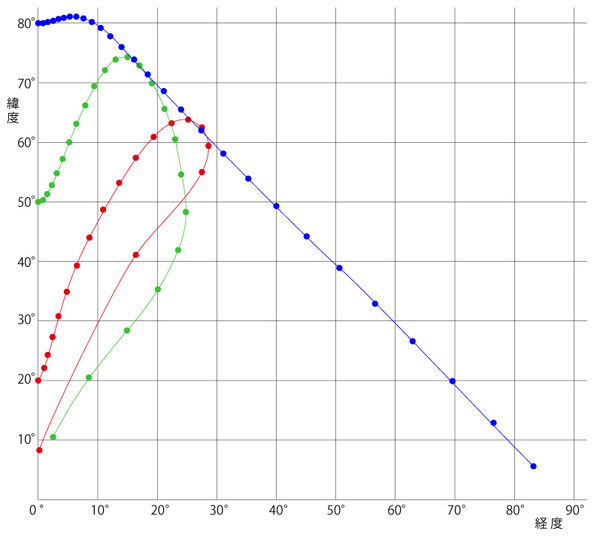
どうしてこのような軌跡になるのか?
答えは, 「ロジックからこれが導かれる!」
しかしこのロジックの数理は,けっこう複雑である。
よってここでは,厳密を端折った簡単な説明をつくってみることにする。
(1) <遠心力>の転向力効果
自転球体の半径を \( R \),角速度を \( \Omega \) とする。
緯度 \( \theta \) の点 \( P \) での遠心力 \( \alpha(\theta) \) は,
\[
\alpha(\theta) = ( R\ cos( \theta )\ \Omega^2
\]
これを \( P \) での接平面に射影した \( \beta (\theta) \) は,
\[
\beta(\theta) = \alpha(\theta) \ sin( \theta ) = R\ \Omega^2\ cos( \theta )\ sin( \theta )
\]
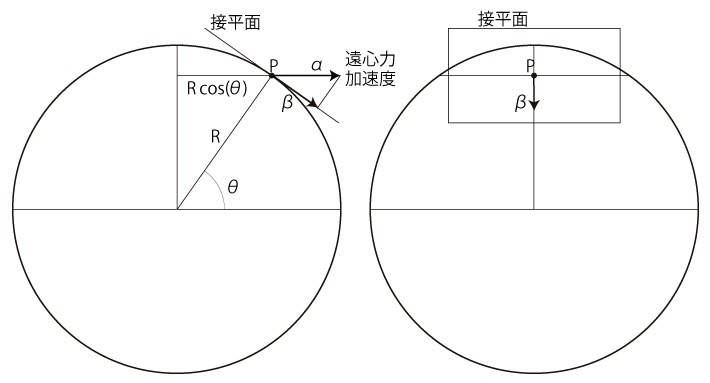
自転球体を地球としたときの \( \beta (\theta) \) を計算してみる。
「地球1周4万km」と「1日24時間」を使って,
\[
R = ( 40000 \times 1000 / 2 ) / \pi \ (m) \\
\Omega = 2 \pi / (24 \times 3600 ) \ (radian/s) \\
\ \\
R\ \Omega^2 = ( ( 40000 \times 1000 / 2 ) / \pi ) \times ( 2 \pi / (24 \times 3600 ) )^2 \\
\quad = ( 40000 \times 1000 ) \times ( 2 \pi ) / (24 \times 3600 )^2 \\
\]
これより,\( \theta \) = 10°, 20°, ‥‥, 80° に対する \( \beta(\theta) \) の値は
| 緯度 |
\( \beta\ (m/s^2) \) |
| 10° |
0.0058 |
| 20° |
0.0108 |
| 30° |
0.0146 |
| 40° |
0.0166 |
| 50° |
0.0166 |
| 60° |
0.0146 |
| 70° |
0.0108 |
| 80° |
0.0058 |
(2) <回転速度の緯度差>の転向力効果
緯度 \( \theta \) の地点の回転速度は,つぎのようになる:

(a) 東向きの移動
球面上の移動の速度は,大円に沿う。
東向きの移動のときは,つぎのようになる:


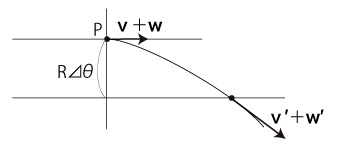
この加速度は,\( {\pmb v} \) に垂直で赤道の方を向く:
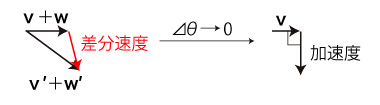
移動には,この加速度に対する慣性加速度として,同じ大きさで逆方向──即ち,極方向──の加速度がかかる。
この加速度は移動方向と直角であり,転向力加速度である。
そして,左向きである。

シミュレーション2のグラフは,移動発進直後の極側への転向と,その模様の緯度差を表している。
それは,この左向き転向力加速度によるものである。
この加速度の大きさは:
\[
- \frac{ d }{ dt } ( R\ cos(\theta)\ \Omega )
= - \frac{ d }{ d\theta } ( R\ cos(\theta)\ \Omega )\ \frac{ d\theta }{ dt } \\
= R\ \Omega\ sin( \theta )\ \frac{ d\theta }{ dt }
\]
自転球体を地球にしたときの \( \gamma( \theta ) = R\ \Omega\ sin( \theta ) \) (単位は \( m / ( radian \cdot s ) \) ) を計算すると:
| 緯度 |
\( \gamma( \theta ) \) |
| 10° |
80 |
| 20° |
158 |
| 30° |
231 |
| 40° |
298 |
| 50° |
355 |
| 60° |
401 |
| 70° |
435 |
| 80° |
456 |
\( d\theta / dt \) の方は,時点ごとに,そのときの移動速度 \( {\pmb v} \) (向きと大きさ) で決まる。
(b) 北向きから東に少しずれた方向の移動
移動による回転速度の変化は,つぎの加速度になる:

移動には,この加速度に対する慣性加速度として,同じ大きさで逆方向の加速度がかかる。
この加速度は移動方向と直角であり,転向力加速度である。
そして,右向きである。

ここでは「東へ」と「北北東へ」の二つの移動を取り上げたが,この例が示すように,移動に働く転向力は──同じ半球でも,移動の方向に依存して──右向きにも左向きにもなる。
気象学は「北半球では右向き」を説いているが,誤りである。
(3) 「北に進み,それから南に方向転換」?
シミュレーショングラフは,「北に進み,それから南に方向転換」模様を現す。
この内容は,「北に進むにつれ速度を減らし,やがてゼロになって折返し」ではない。
移動の転向は,軌道の大円の変更である。
この軌道大円変更の連続が,グラフでは「北に進み,それから南に方向転換」のように見えるということである。
|